12  不平等度量

在经济学和社会科学领域，衡量收入或财富分配的不平等程度是一个重要的研究课题。为了量化这种不平等，研究人员开发了多种统计指标，其中最常用的两个是基尼系数和泰尔指数。

加载包：

library(tidyverse)
library(mathmodels)

12.1 个体数据与平均数据

个体数据，就是每个人占一行，记录其收入；（分组）平均数据，是将人按某分组变量（如部门）分组，每组一行，记录该组的平均收入和人数。

比如，这是 5 名员工的个体数据：

df = tibble(dep = c(rep("技术部", 3), rep("销售部", 2)),
            emp = LETTERS[1:5], 
            income = c(10, 12, 20, 5, 8))
df

# A tibble: 5 × 3
  dep    emp   income
  <chr>  <chr>  <dbl>
1 技术部 A         10
2 技术部 B         12
3 技术部 C         20
4 销售部 D          5
5 销售部 E          8

按部门分组汇总，计算每个部门的人均收入和人数，就得到平均数据：

df |> 
  summarise(income = mean(income), pop = n(), .by = dep)

# A tibble: 2 × 3
  dep    income   pop
  <chr>   <dbl> <int>
1 技术部   14       3
2 销售部    6.5     2

最常见的平均数据，就是人均指标和人口数的数据，也称为人口加权数据。

计算基尼系数或泰尔指数时，需要区分个体数据和平均数据（人口加权数据），二者的计算公式是不同的。

12.2 基尼系数

基尼系数，通过洛伦茨曲线计算，反映实际收入分布与完全平等线之间的面积比例。该指标直观且易于理解，但对中间群体的变化较为敏感，而对极端值的敏感性相对不足。

12.2.1 洛伦兹曲线与基尼系数

洛伦兹曲线，是一种用来展示社会中收入或财富的分配情况的曲线图。具体来说，它展示的是：

• x 轴：表示人口的累计百分比，从最贫穷的人到最富有的人排列。
• y 轴：表示收入或财富的累计百分比。

洛伦兹曲线与基尼系数

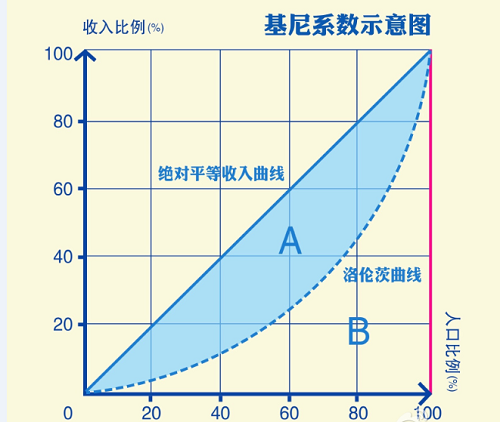
基尼系数，通过洛伦兹曲线与绝对平等线之间的面积来衡量不平等性。具体来说：

• 如果洛伦兹曲线与绝对平等线之间的面积越大，表示不平等性越高。
• 基尼系数实际上就是该面积的量化，是介于 \(0\) 到 \(1\) 之间的数值。

具体解释：

• \(\text{基尼系数 } = 0\)：意味着绝对平等，所有人的收入或财富是完全一样的。洛伦兹曲线和绝对平等线重合，没有差距。
• \(\text{基尼系数 } = 1\)：意味着绝对不平等，所有收入或财富都集中在一个人的手里。洛伦兹曲线向下弯到几乎贴近 x 轴和 y 轴，除了一个点之外，其他人都几乎没有收入或财富。

12.2.2 基尼系数计算方法

1. 针对个体数据（比如个体收入向量）： \[ Gini = \frac{\sum_{i=1}^n\sum_{i=1}^n|x_i-x_j|}{2n^2\bar{x}} \]

mathmodels 包提供了 gini0() 函数按上述公式计算个体数据的基尼系数，基本语法：

gini0(y)

• y 为个体收入向量。

2. 针对平均数据：即面积法，利用数值积分，近似计算绝对平等线与洛伦兹曲线围成的面积。

记平均收入向量 \(\mathbf{I} = (I_1, I_2, \ldots, I_n)\) 和人口向量 \(\mathbf{P} = (P_1, P_2, \ldots, P_n)\)。

• 对 \(\mathbf{I} / \mathbf{P}\) 从小到大排序，按排序索引重排 \(\mathbf{I}\) 和 \(\mathbf{P}\)，为了简便仍记为 \(\mathbf{I}\) 和 \(\mathbf{P}\)。

• 计算累积人口比例和累积收入比例： \[ x_k = \frac{\sum_{i=1}^k P_i}{\sum_{i=1}^n P_i}, \quad y_k = \frac{\sum_{i=1}^k I_i}{\sum_{i=1}^n I_i} \] 其中，\(k = 0, 1, \cdots, n\) 且 \(x_0 = y_0 = 0\)。

• 用梯形法数值积分计算洛伦兹曲线下面积：
  \[ A = \sum_{i=1}^n \frac{(x_i - x_{i-1}) \cdot (y_i + y_{i-1})}{2} \]

• 绝对平等线下面积为 \(0.5\)，基尼系数为两面积之差与绝对平等线面积的比值： \[ G = \frac{0.5 - A}{0.5} = 1 - 2A \]

mathmodels 包提供了 gini() 函数按上述步骤计算平均数据的基尼系数，基本语法：

gini(y, pop)

• y 和 pop 分别为各分组的人均收入和人口数构成的向量。

12.2.3 案例：批量计算基尼系数

数据整理自国家统计局网站，包含 2014-2023 年全国 31 个省份八个主要行业：“信息业”、“制造业”、“医疗”、“商贸”、“建筑业”、“教育”、“科研”、“金融业”的平均工资和就业人数。

df = readxl::read_excel("data/income.xlsx")
df

# A tibble: 2,480 × 6
   行业   区域  地区   年份 平均工资 就业人数
   <chr>  <chr> <chr> <dbl>    <dbl>    <dbl>
 1 信息业 东部  上海   2014   170174   248000
 2 信息业 东部  上海   2015   183365   254000
 3 信息业 东部  上海   2016   200657   268000
 4 信息业 东部  上海   2017   212063   307000
 5 信息业 东部  上海   2018   232522   356000
 6 信息业 东部  上海   2019   237405   418000
 7 信息业 东部  上海   2020   270619   448000
 8 信息业 东部  上海   2021   303573   507000
 9 信息业 东部  上海   2022   330126   544000
10 信息业 东部  上海   2023   363745   528000
# ℹ 2,470 more rows

1. 每个行业每年份内省份间工资的不平等程度（基尼系数）

• 就是简单的分组汇总：按 年份 和 行业 分组，每组计算出一个基尼系数值

res = df |> 
  summarise(Gini = gini(平均工资, 就业人数), .by = c(年份, 行业)) 
res 

# A tibble: 80 × 3
    年份 行业    Gini
   <dbl> <chr>  <dbl>
 1  2014 信息业 0.410
 2  2015 信息业 0.432
 3  2016 信息业 0.435
 4  2017 信息业 0.449
 5  2018 信息业 0.457
 6  2019 信息业 0.452
 7  2020 信息业 0.456
 8  2021 信息业 0.477
 9  2022 信息业 0.472
10  2023 信息业 0.483
# ℹ 70 more rows

• 结果是整洁长表，接着做可视化非常容易：

res |> 
  ggplot(aes(年份, Gini, color = 行业)) +
  geom_line() +
  geom_point() +
  theme_minimal()

• 若想结果更适合人类阅读，再来个长变宽：

res |> 
  pivot_wider(names_from = 行业, values_from = Gini)

# A tibble: 10 × 9
    年份 信息业 制造业  医疗  商贸 建筑业  教育  科研 金融业
   <dbl>  <dbl>  <dbl> <dbl> <dbl>  <dbl> <dbl> <dbl>  <dbl>
 1  2014  0.410  0.533 0.355 0.379  0.498 0.373 0.324  0.329
 2  2015  0.432  0.535 0.361 0.384  0.499 0.375 0.343  0.333
 3  2016  0.435  0.540 0.355 0.387  0.502 0.364 0.353  0.349
 4  2017  0.449  0.551 0.346 0.389  0.514 0.357 0.357  0.348
 5  2018  0.457  0.555 0.349 0.382  0.533 0.344 0.363  0.360
 6  2019  0.452  0.560 0.344 0.392  0.501 0.354 0.381  0.353
 7  2020  0.456  0.563 0.349 0.374  0.514 0.367 0.358  0.369
 8  2021  0.477  0.560 0.344 0.379  0.509 0.368 0.366  0.366
 9  2022  0.472  0.557 0.346 0.381  0.522 0.369 0.378  0.355
10  2023  0.483  0.559 0.353 0.398  0.543 0.370 0.394  0.337

2. 每个省份每年份内行业间工资的不平等程度（基尼系数）

df |> 
  summarise(Gini = gini(平均工资, 就业人数), .by = c(年份, 地区)) |> 
  pivot_wider(names_from = 地区, values_from = Gini)

# A tibble: 10 × 32
    年份  上海  云南 内蒙古  北京  吉林  四川  天津  宁夏  安徽  山东  山西
   <dbl> <dbl> <dbl>  <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
 1  2014 0.542 0.541  0.423 0.325 0.484 0.546 0.637 0.471 0.522 0.613 0.475
 2  2015 0.525 0.546  0.423 0.305 0.484 0.525 0.601 0.461 0.521 0.603 0.455
 3  2016 0.501 0.538  0.411 0.276 0.471 0.508 0.566 0.446 0.510 0.589 0.450
 4  2017 0.478 0.536  0.378 0.261 0.441 0.500 0.517 0.448 0.508 0.575 0.455
 5  2018 0.457 0.527  0.356 0.226 0.407 0.515 0.479 0.427 0.537 0.559 0.438
 6  2019 0.393 0.433  0.334 0.151 0.357 0.517 0.460 0.399 0.502 0.504 0.410
 7  2020 0.403 0.436  0.348 0.130 0.347 0.481 0.438 0.397 0.491 0.477 0.399
 8  2021 0.397 0.426  0.377 0.138 0.365 0.465 0.417 0.407 0.506 0.475 0.402
 9  2022 0.377 0.424  0.385 0.136 0.373 0.462 0.429 0.439 0.527 0.486 0.410
10  2023 0.360 0.434  0.402 0.137 0.390 0.425 0.441 0.484 0.533 0.474 0.405
# ℹ 20 more variables: 广东 <dbl>, 广西 <dbl>, 新疆 <dbl>, 江苏 <dbl>,
#   江西 <dbl>, 河北 <dbl>, 河南 <dbl>, 浙江 <dbl>, 海南 <dbl>, 湖北 <dbl>,
#   湖南 <dbl>, 甘肃 <dbl>, 福建 <dbl>, 西藏 <dbl>, 贵州 <dbl>, 辽宁 <dbl>,
#   重庆 <dbl>, 陕西 <dbl>, 青海 <dbl>, 黑龙江 <dbl>

12.2.4 绘制洛伦兹曲线

以“教育”行业 2023 年的数据为例，

edu23 = df |> 
  filter(行业 == "教育", 年份 == "2023")
edu23

# A tibble: 31 × 6
   行业  区域  地区    年份 平均工资 就业人数
   <chr> <chr> <chr>  <dbl>    <dbl>    <dbl>
 1 教育  东部  上海    2023   235503   388000
 2 教育  西部  云南    2023   116750   644000
 3 教育  西部  内蒙古  2023   110236   366000
 4 教育  东部  北京    2023   230965   508000
 5 教育  东北  吉林    2023   100625   346000
 6 教育  西部  四川    2023   116527  1238000
 7 教育  东部  天津    2023   149140   212000
 8 教育  西部  宁夏    2023   111737   112000
 9 教育  中部  安徽    2023   119779   678000
10 教育  东部  山东    2023   124519  1291000
# ℹ 21 more rows

洛伦兹曲线（也是计算基尼系数），关键的一步是按 x / pop 排序，注意不是按平均收入 x 排序，然后计算人口数和平均收入的累计百分比，分别作为 x 轴和 y 轴绘图即可。

edu23 |>
  arrange(平均工资 / 就业人数) |>
  mutate(frac_pop = cumsum(就业人数) / sum(就业人数), 
         frac_inc = cumsum(平均工资) / sum(平均工资)) |>
  ggplot(aes(frac_pop, frac_inc)) +
  geom_line() +
  geom_polygon(fill = "grey70") +
  coord_equal() +
  theme_bw() +
  labs(x = "累计人数百分比", y = "累计收入百分比")

• 再看一下，该洛伦兹曲线对应的基尼系数值：

gini(edu23$平均工资,edu23$就业人数)

[1] 0.3697145

12.3 泰尔指数

泰尔指数，是一种基于信息理论的不平等度量方法，其核心思想是衡量收入分布偏离“完全平等”状态的信息熵。泰尔指数的一个显著优点是它可以自然地分解为组间和组内不平等，从而便于分析不同层次（如省、市）对总体不平等的贡献。

12.3.1 总体泰尔指数

(1) 针对个体数据

\[ T=\frac1n\sum\limits_{i=1}^n\frac{Y_i}{\overline{Y}}\ln(\frac{Y_i}{\overline{Y}})=\sum\limits_{i=1}^n\frac{Y_i}{Y}\ln(\frac{Y_i}{\overline{Y}})=\sum\limits_{i=1}^n\frac{Y_i}{Y}\ln(\frac{Y_i/Y}{1/n}) \] 其中，\(T\) 为总体泰尔指数，\(Y_i\) 表示第 \(i\) 个体的收入，\(\overline{Y}\) 表示所有个体的平均收入，\(Y\) 表示所有个体的总收入。

三个表达式，按哪个计算都可以。

mathmodels 包提供了 theil0()函数计算个体数据的总体泰尔指数，基本语法：

theil0(y)

• y 为个体收入向量。

(2) 针对平均数据（人口加权数据）

\[ T=\sum\limits_i\frac{Y_i}Y\ln\frac{Y_i/Y}{N_i/N}=\sum\limits_i\frac{N_i}N\frac{\overline{Y}_i}{\overline{Y}}\ln\frac{\overline{Y}_i}{\overline{Y}} \] 其中，\(Y_i, \, N_i\) 分别表示第 \(i\) 组的总收入和总人口，\(Y, \, N\) 分别表示所有组的总收入和总人口，故 \(\frac{Y_i}{Y}\) 表示第 \(i\) 组收入占总收入的比重，\(\frac{N_i}{N}\) 表示第 \(i\) 组人口数占总人口数的比重。

总收入当然等于人口数乘以平均收入，所以，引入 \(\overline{Y_i}, \, \overline{Y}\) 改写为第 2 式，以与平均数据相对应。

mathmodels 包提供了 theil()函数计算个体数据的总体泰尔指数，基本语法：

theil(y, pop)

• y 和 pop 分别为各分组的人均收入和人口数构成的向量。

12.3.2 单分组变量的泰尔指数及其分解

泰尔指数分解，就是总体泰尔指数关于单个分组变量 g 分解为组内和组间泰尔指数，同样也需要区分：个体数据和平均数据。

总体泰尔指数，当然可以忽略分组，直接按个体数据或平均数据的计算公式计算。因为要做分解，故可采用分解后的组内与组间泰尔指数加和得到总体泰尔指数： \[ T = T_w + T_b \]

从逻辑上叙述清楚比摆一堆公式更好理解，泰尔指数分解计算步骤如下：

1. 数据关于分组变量 g 分为多组，分别对第 \(i\) 组的数据，计算每组的总体泰尔指数即 \(T_{wi}\) （根据个体数据/平均数据选用相应的前文公式即可）；

2. 组内泰尔指数 \(T_w\) 就是每组的总体泰尔指数关于各组收入对总收入占比的加权和： \[ T_w = \sum\limits_i \frac{Y_i}{Y} T_{wi} \]

3. 组间泰尔指数 \(T_b\)，是对原始数据按分组变量 g 分组汇总到各组的平均收入和人口数，再计算总体泰尔指数（此时一定是平均数据）；

4. 进一步，可以计算第 \(i\) 组组内差距的贡献率以及组内、组间差距的贡献率： \[ R_{wi}=\frac{Y_i}Y*\frac{T_{wi}}T=\frac{N_i}N\frac{\overline{Y}_i}{\overline{Y}}*\frac{T_{wi}}T \] \[ R_w = \frac{T_w}{T}, \quad R_b = \frac{T_b} T \]

这些贡献率满足：\(R_w = \sum\limits_i R_{wi}, \, R_w + R_b = 1\)。

mathmodels 包提供了 theil0_g() 和 theil_g() 函数，分别针对个体数据和平均数据，关于一个分组变量计算泰尔指数及其分解，基本语法：

theil0_g(data, group, y)
theil_g(data, group, y, pop)

• data 为包含所需变量的数据框；
• group 为单个分组变量的名字；
• y 和 pop 分别为各分组的人均收入和人口数构成的向量。

返回包含两个成分的列表：

• theil: 总体、组间、组内、每个分组的泰尔指数；
• ratio: 相应的贡献率。

12.3.3 两分组变量的泰尔指数及其分解

1. 两交叉分组变量的泰尔指数及其分解

对于两个交叉分组变量，例如 group1（如行业）和 group2（如区域：东部、中部、西部），是对单分组变量泰尔指数分解的扩展。总体泰尔指数仍分解为基于 group1 的组间和组内部分，但组内部分进一步分解为基于 group2 的组间和组内贡献，从而提供交叉分组下更细致的不平等分析。

组内泰尔指数（Tw）及其分解，目的是衡量 group1 内部的不平等，并按 group2 进一步分解。对每个 group1 分组，

• group2 组间泰尔指数：

在该 group1 内按 group2（如区域）汇总数据。计算每 group2 的平均收入和人口。使用泰尔公式计算： \[ T_{g2b} = \sum_j \left( \frac{Y_{ij}}{Y_i} \right) \ln \left( \frac{Y_{ij} / N_{ij}}{Y_i / N_i} \right) \] 其中，\(Y_{ij}\) 和 \(N_{ij}\) 是 group1 内 group2 第 \(j\) 组的收入和人口。

• group2 组内泰尔指数

若 group2 内有更细的数据（如区域内的省份），计算每 group2 单元的泰尔指数，并按人口占比加权： \[ T_{g2w} = \sum_j \left( \frac{N_{ij}}{N_i} \right) T_{wij} \] 其中，\(T_{wij}\) 是 group2 第 j 组内的泰尔指数（若仅为平均数据，T_{g2w} 为 \(0\)）。

mathmodels 包提供了 theil_g2_cross() 函数实现两交叉分组变量的泰尔指数及其分解，基本语法：

theil_g2_cross(data, group1, group2, y, pop)

• data 为包含所需变量的数据框；
• group1 和 group2 分别为交叉的第一和第二分组变量的名字；
• y 和 pop 分别为各分组的人均收入和人口数构成的向量。

返回包含两个成分的列表：

• theil: 总体、group1 组间、group1 组内、group2 组间、group2 组内、每个 group1 分组的组内泰尔指数；
• ratio: 相应的贡献率。

2. 两嵌套分组变量的泰尔指数及其分解

对于两嵌套分组变量 group1 和 group2，其中 group2 嵌套在 group1 内（比如省嵌套市），总体泰尔指数分解为基于 group1 的组间不平等、基于 group2 的组间不平等以及 group2 内的组内不平等。与两交叉分组变量不同，嵌套结构的泰尔指数分解更侧重于层次结构。

(1) group1 组间泰尔指数（衡量 group1 各分组之间的不平等）

按 group1 汇总数据，计算每组的总收入和总人口，计算组级平均收入，使用平均数据的泰尔公式计算。

(2) group2 组间泰尔指数（衡量每个 group1 内 group2 各分组之间的不平等）

在每个 group1 分组下，计算每个 group2 分组的平均收入和总人口，计算分泰尔指数： \[ T_b^{g2i} = \sum_j \left( \frac{Y_{ij}}{Y_i} \right) \ln \left( \frac{Y_{ij} / N_{ij}}{Y_i / N_i} \right) \] 其中，\(Y_{ij}\) 和 \(N_{ij}\) 是 group1 内 group2 第 \(j\) 分组的收入和人口，\(Y_i\) 和 \(N_i\) 是该 group1 的总收入和人口。

若某 group1 内仅有一个 group2，则 \(T_b^{g2i} = 0\)。

总体 \(T_b^{g2}\) 为各 group1 的 \(T_b^{g2i}\) 加权和： \[ T_b^{g2} = \sum_i \left( \frac{Y_i}{Y} \right) T_b^{g2i} \]

(3) group2 组内泰尔指数（衡量每个 group2 分组内部的不平等）

按 group1 和 group2 分组数据，计算每个分组内个体数据的泰尔指数 \(T_w^{ij}\)（若为平均数据，\(T_w^{ij} = 0\)）。

总体 \(T_w\) 为各 group2 \(T_w^{ij}\) 的加权和： \[ T_w = \sum_i \sum_j \left( \frac{Y_{ij}}{Y} \right) T_w^{ij} \]

mathmodels 包提供了 theil_g2_nest() 函数实现两交叉分组变量的泰尔指数及其分解，基本语法：

theil_g2_nest(data, group1, group2, y, pop)

• data 为包含所需变量的数据框；
• group1 和 group2 分别为嵌套的第一和第二分组变量的名字；
• y 和 pop 分别为各分组的人均收入和人口数构成的向量。

返回包含两个成分的列表：

• theil: 总体、group1 组间、group2 组间、group2 组内、每个 group1/group2 分组的组内泰尔指数；
• ratio: 相应的贡献率。

总结区分：

• 单分组变量仅将总体泰尔指数分解为组间部分 \(T_b\) 和组内部分 \(T_w\)，无进一步细分。
• 两交叉分组变量将组内部分 \(T_w\) 分解为 \(T_{wb}\)（group2 组间）和 \(T_{ww}\)（group2 组内），强调 group2 在 group1 内的交叉作用。
• 两嵌套分组将组间部分 \(T_b\) 分为 \(T_{b1}\)（ group1 间）和 \(T_{b2}\)（ group2 间），\(T_w\) 仅为 group2 内的不平等，反映严格的层次结构。

12.3.4 案例：批量计算泰尔指数及其分解

仍使用前文的 2014-2023 年全国 31 个省份八个主要行业的平均工资和就业人数数据。

1. 每年关于行业的收入不平等性（泰尔指数及其分解）

theil_*() 系列函数的返回值，特意设计为两个成分的列表，且每个成分是长度相同、元素命名相同的向量，非常方便分组汇总并展开批量结果。

每年就是按年份分组汇总，关于行业就是以 行业 为分组变量，分别对每组数据计算关于单个分组变量的泰尔指数及其分解。因为每组返回长度为 \(2\) 的对象（列表），所以用 reframe() 代替 summarise()，结果是行数翻倍。

res = df |> 
  reframe(Theil = theil_g(pick(everything()), group = "行业", 
                          y = "平均工资", pop = "就业人数"), 
          .by = 年份) 
res 

# A tibble: 20 × 2
    年份 Theil       
   <dbl> <named list>
 1  2014 <dbl [11]>  
 2  2014 <dbl [11]>  
 3  2015 <dbl [11]>  
 4  2015 <dbl [11]>  
 5  2016 <dbl [11]>  
 6  2016 <dbl [11]>  
 7  2017 <dbl [11]>  
 8  2017 <dbl [11]>  
 9  2018 <dbl [11]>  
10  2018 <dbl [11]>  
11  2019 <dbl [11]>  
12  2019 <dbl [11]>  
13  2020 <dbl [11]>  
14  2020 <dbl [11]>  
15  2021 <dbl [11]>  
16  2021 <dbl [11]>  
17  2022 <dbl [11]>  
18  2022 <dbl [11]>  
19  2023 <dbl [11]>  
20  2023 <dbl [11]>  

Theil 列是嵌套的向量，再做横向（往宽）展开即可：

res |> 
  unnest_wider(Theil)

# A tibble: 20 × 12
    年份      T     Tb     Tw 信息业 制造业   医疗   商贸 建筑业   教育   科研
   <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>
 1  2014 0.0609 0.0304 0.0305 0.0641 0.0148 0.0400 0.0660 0.0111 0.0243 0.0591
 2  2014 1      0.499  0.501  0.0490 0.0897 0.0461 0.0735 0.0334 0.0535 0.0447
 3  2015 0.0628 0.0326 0.0302 0.0603 0.0157 0.0339 0.0654 0.0113 0.0193 0.0511
 4  2015 1      0.519  0.481  0.0476 0.0885 0.0411 0.0701 0.0312 0.0449 0.0377
 5  2016 0.0633 0.0331 0.0302 0.0600 0.0170 0.0314 0.0669 0.0112 0.0187 0.0483
 6  2016 1      0.522  0.478  0.0497 0.0919 0.0404 0.0706 0.0295 0.0449 0.0364
 7  2017 0.0663 0.0348 0.0315 0.0598 0.0169 0.0322 0.0681 0.0122 0.0206 0.0445
 8  2017 1      0.525  0.475  0.0520 0.0831 0.0428 0.0674 0.0297 0.0492 0.0334
 9  2018 0.0670 0.0350 0.0319 0.0599 0.0156 0.0338 0.0681 0.0122 0.0221 0.0416
10  2018 1      0.523  0.477  0.0570 0.0710 0.0459 0.0684 0.0304 0.0538 0.0320
11  2019 0.0684 0.0333 0.0352 0.0666 0.0162 0.0412 0.0661 0.0147 0.0260 0.0439
12  2019 1      0.486  0.514  0.0675 0.0668 0.0624 0.0673 0.0302 0.0670 0.0351
13  2020 0.0718 0.0333 0.0386 0.0711 0.0163 0.0399 0.0774 0.0157 0.0308 0.0431
14  2020 1      0.463  0.537  0.0758 0.0633 0.0596 0.0720 0.0290 0.0790 0.0320
15  2021 0.0759 0.0352 0.0407 0.0683 0.0169 0.0387 0.0762 0.0171 0.0323 0.0443
16  2021 1      0.463  0.537  0.0758 0.0635 0.0568 0.0693 0.0270 0.0751 0.0321
17  2022 0.0835 0.0411 0.0425 0.0697 0.0182 0.0396 0.0827 0.0200 0.0304 0.0452
18  2022 1      0.492  0.508  0.0744 0.0608 0.0548 0.0686 0.0264 0.0655 0.0309
19  2023 0.0810 0.0406 0.0403 0.0693 0.0162 0.0375 0.0768 0.0173 0.0326 0.0452
20  2023 1      0.502  0.498  0.0777 0.0550 0.0557 0.0683 0.0222 0.0718 0.0320
# ℹ 1 more variable: 金融业 <dbl>

每个年份，第一行是总体、行业间、行业内泰尔指数，各行业的（总体）泰尔指数；第二行是相应的贡献率，各行业贡献率之和等于行业内贡献率，行业间贡献率 \(+\) 行业内贡献率 \(= 1\)。

2. 每年关于区域的收入不平等性（批量泰尔指数及其分解）

同样做法，只需将分组变量换成 区域：

df |> 
  reframe(Theil = theil_g(pick(everything()), group = "区域", 
                          y = "平均工资", pop = "就业人数"), 
          .by = 年份) |> 
  unnest_wider(Theil)

# A tibble: 20 × 8
    年份      T      Tb     Tw   东部   西部    东北   中部
   <dbl>  <dbl>   <dbl>  <dbl>  <dbl>  <dbl>   <dbl>  <dbl>
 1  2014 0.0609 0.00915 0.0517 0.0732 0.0263 0.0156  0.0150
 2  2014 1      0.150   0.850  0.718  0.0751 0.0150  0.0417
 3  2015 0.0628 0.00900 0.0538 0.0754 0.0283 0.0180  0.0175
 4  2015 1      0.143   0.857  0.713  0.0800 0.0161  0.0477
 5  2016 0.0633 0.00908 0.0542 0.0748 0.0294 0.0166  0.0209
 6  2016 1      0.143   0.857  0.702  0.0831 0.0138  0.0575
 7  2017 0.0663 0.00939 0.0570 0.0779 0.0312 0.0159  0.0239
 8  2017 1      0.142   0.858  0.699  0.0850 0.0118  0.0629
 9  2018 0.0670 0.00859 0.0584 0.0804 0.0298 0.0128  0.0232
10  2018 1      0.128   0.872  0.724  0.0798 0.00885 0.0596
11  2019 0.0684 0.0119  0.0565 0.0791 0.0251 0.0111  0.0217
12  2019 1      0.174   0.826  0.698  0.0659 0.00738 0.0541
13  2020 0.0718 0.0130  0.0588 0.0836 0.0234 0.0105  0.0210
14  2020 1      0.181   0.819  0.703  0.0604 0.00630 0.0489
15  2021 0.0759 0.0144  0.0615 0.0861 0.0245 0.00839 0.0236
16  2021 1      0.190   0.810  0.696  0.0587 0.00454 0.0511
17  2022 0.0835 0.0159  0.0676 0.0942 0.0264 0.00920 0.0272
18  2022 1      0.191   0.809  0.694  0.0575 0.00441 0.0528
19  2023 0.0810 0.0140  0.0670 0.0953 0.0223 0.00920 0.0243
20  2023 1      0.172   0.828  0.724  0.0506 0.00453 0.0482

每个年份，第一行是总体、区域间、区域内泰尔指数，各区域的（总体）泰尔指数；第二行是相应的贡献率，各区域贡献率之和等于区域内贡献率，区域间贡献率 \(+\) 区域内贡献率 \(= 1\)。

3. 两交叉分组泰尔指数及其分解

批量计算每年 行业 与 区域 两交叉分组泰尔指数及其分解：

df |> 
  reframe(Theil = theil_g2_cross(pick(everything()), 
                                 group1 = "行业", group2 = "区域", 
                                 y = "平均工资", pop = "就业人数"), 
          .by = 年份) |> 
  unnest_wider(Theil)

# A tibble: 20 × 14
    年份      T     Tb     Tw   Tw_b   Tw_w 信息业 制造业   医疗   商贸 建筑业
   <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>
 1  2014 0.0590 0.0304 0.0286 0.0129 0.0157 0.0612 0.0144 0.0369 0.0599 0.0108
 2  2014 1      0.515  0.485  0.219  0.266  0.0483 0.0902 0.0439 0.0689 0.0335
 3  2015 0.0609 0.0326 0.0283 0.0128 0.0155 0.0578 0.0152 0.0316 0.0595 0.0110
 4  2015 1      0.535  0.465  0.210  0.255  0.0471 0.0884 0.0395 0.0657 0.0312
 5  2016 0.0615 0.0331 0.0285 0.0129 0.0156 0.0584 0.0165 0.0294 0.0609 0.0109
 6  2016 1      0.537  0.463  0.209  0.253  0.0498 0.0916 0.0390 0.0661 0.0294
 7  2017 0.0644 0.0348 0.0295 0.0133 0.0163 0.0576 0.0163 0.0299 0.0618 0.0118
 8  2017 1      0.541  0.459  0.206  0.253  0.0517 0.0830 0.0410 0.0630 0.0294
 9  2018 0.0650 0.0350 0.0300 0.0127 0.0173 0.0577 0.0151 0.0315 0.0620 0.0118
10  2018 1      0.539  0.461  0.196  0.265  0.0565 0.0711 0.0440 0.0641 0.0302
11  2019 0.0663 0.0333 0.0330 0.0153 0.0178 0.0639 0.0157 0.0383 0.0604 0.0140
12  2019 1      0.502  0.498  0.231  0.268  0.0669 0.0668 0.0599 0.0635 0.0297
13  2020 0.0693 0.0333 0.0361 0.0169 0.0192 0.0680 0.0159 0.0376 0.0700 0.0150
14  2020 1      0.480  0.520  0.243  0.277  0.0751 0.0636 0.0581 0.0675 0.0287
15  2021 0.0731 0.0352 0.0380 0.0171 0.0209 0.0659 0.0164 0.0365 0.0692 0.0163
16  2021 1      0.481  0.519  0.233  0.286  0.0758 0.0639 0.0557 0.0652 0.0267
17  2022 0.0807 0.0411 0.0397 0.0187 0.0210 0.0670 0.0176 0.0375 0.0747 0.0190
18  2022 1      0.509  0.491  0.231  0.260  0.0741 0.0610 0.0536 0.0642 0.0259
19  2023 0.0783 0.0406 0.0377 0.0171 0.0206 0.0663 0.0157 0.0353 0.0694 0.0166
20  2023 1      0.519  0.481  0.218  0.263  0.0768 0.0552 0.0542 0.0639 0.0221
# ℹ 3 more variables: 教育 <dbl>, 科研 <dbl>, 金融业 <dbl>

注意分解关系：

• 泰尔指数：T = Tb + Tw，Tw = Tw_b + Tw_w

• 贡献率：R_Tw = R_Tw_b + R_Tw_w = R_T_信息业 + ... + R_T_金融业

4. 两嵌套分组泰尔指数及其分解

仅用数据中有嵌套关系的 区域 和 地区 测试：

df |> 
  reframe(Theil = theil_g2_nest(pick(everything()), 
                                group1 = "区域", group2 = "地区", 
                                y = "平均工资", pop = "就业人数"), 
          .by = 年份) |> 
  unnest_wider(Theil)

# A tibble: 20 × 40
    年份      T   Tb_g1  Tb_g2     Tw   东部    西部      东北    中部 东部_上海
   <dbl>  <dbl>   <dbl>  <dbl>  <dbl>  <dbl>   <dbl>     <dbl>   <dbl>     <dbl>
 1  2014 0.0609 0.00915 0.0234 0.0283 0.0374 0.00286 0.000441  0.00308    0.0547
 2  2014 1      0.150   0.384  0.465  0.367  0.00818 0.000425  0.00858    0.0573
 3  2015 0.0628 0.00900 0.0233 0.0305 0.0373 0.00321 0.000148  0.00331    0.0529
 4  2015 1      0.143   0.371  0.486  0.353  0.00909 0.000132  0.00904    0.0522
 5  2016 0.0633 0.00908 0.0230 0.0312 0.0369 0.00271 0.000187  0.00334    0.0505
 6  2016 1      0.143   0.364  0.493  0.347  0.00765 0.000155  0.00921    0.0499
 7  2017 0.0663 0.00939 0.0236 0.0334 0.0382 0.00203 0.000352  0.00267    0.0494
 8  2017 1      0.142   0.355  0.503  0.342  0.00553 0.000262  0.00702    0.0472
 9  2018 0.0670 0.00859 0.0253 0.0331 0.0407 0.00197 0.000638  0.00230    0.0455
10  2018 1      0.128   0.378  0.494  0.366  0.00528 0.000442  0.00589    0.0439
11  2019 0.0684 0.0119  0.0260 0.0305 0.0417 0.00194 0.000469  0.00237    0.0351
12  2019 1      0.174   0.380  0.446  0.369  0.00509 0.000313  0.00592    0.0361
13  2020 0.0718 0.0130  0.0272 0.0316 0.0436 0.00199 0.000969  0.00310    0.0430
14  2020 1      0.181   0.379  0.439  0.366  0.00514 0.000584  0.00723    0.0418
15  2021 0.0759 0.0144  0.0294 0.0321 0.0459 0.00234 0.000409  0.00473    0.0502
16  2021 1      0.190   0.387  0.423  0.371  0.00560 0.000221  0.0103     0.0501
17  2022 0.0835 0.0159  0.0314 0.0362 0.0489 0.00231 0.000311  0.00489    0.0522
18  2022 1      0.191   0.375  0.434  0.361  0.00503 0.000149  0.00948    0.0499
19  2023 0.0810 0.0140  0.0319 0.0351 0.0499 0.00254 0.0000470 0.00450    0.0490
20  2023 1      0.172   0.394  0.433  0.380  0.00578 0.0000231 0.00894    0.0486
# ℹ 30 more variables: 西部_云南 <dbl>, 西部_内蒙古 <dbl>, 东部_北京 <dbl>,
#   东北_吉林 <dbl>, 西部_四川 <dbl>, 东部_天津 <dbl>, 西部_宁夏 <dbl>,
#   中部_安徽 <dbl>, 东部_山东 <dbl>, 中部_山西 <dbl>, 东部_广东 <dbl>,
#   西部_广西 <dbl>, 西部_新疆 <dbl>, 东部_江苏 <dbl>, 中部_江西 <dbl>,
#   东部_河北 <dbl>, 中部_河南 <dbl>, 东部_浙江 <dbl>, 东部_海南 <dbl>,
#   中部_湖北 <dbl>, 中部_湖南 <dbl>, 西部_甘肃 <dbl>, 东部_福建 <dbl>,
#   西部_西藏 <dbl>, 西部_贵州 <dbl>, 东北_辽宁 <dbl>, 西部_重庆 <dbl>, …

注意分解关系：

• 泰尔指数：T = Tb_g1 + Tb_g2 + Tw

• 贡献率：R_Tb_g2 = R_东部 + ... + R_中部，R_Tw = R_东部_上海 + ... + R_东北_黑龙江