2  层次分析法

层次分析法（AHP），是一种将复杂决策问题结构化并进行定量分析的系统方法，由美国运筹学家 T. L. Saaty 于 20 世纪 70 年代提出。该方法通过构建层次结构模型，并对主观判断进行量化处理，从而有效解决多目标、多准则下的复杂决策问题，尤其适用于定性因素与定量因素交织的实际场景。

AHP 的核心优势在于能够合理地结合定性判断与定量分析，依据人类思维和心理规律，将决策过程层次化、数量化，使原本模糊的判断变得清晰可操作。因此，它被广泛应用于各类复杂的决策分析中。由于其决策依据主要来源于计算所得的权重，AHP 也常被用于确定评价指标的相对重要性权重。

与传统依赖大量定量数据的方法不同，AHP 只需通过对指标之间的定性比较，即可构造判断矩阵并进一步合成得出各指标的权重，也因此是一种主观赋权法。在实际应用中，建议采用问卷形式，邀请多位专家对各项指标进行两两比较或直接打分，从而构建出更具代表性和科学性的判断矩阵。

2.1 算法步骤

2.1.1 建立层次结构

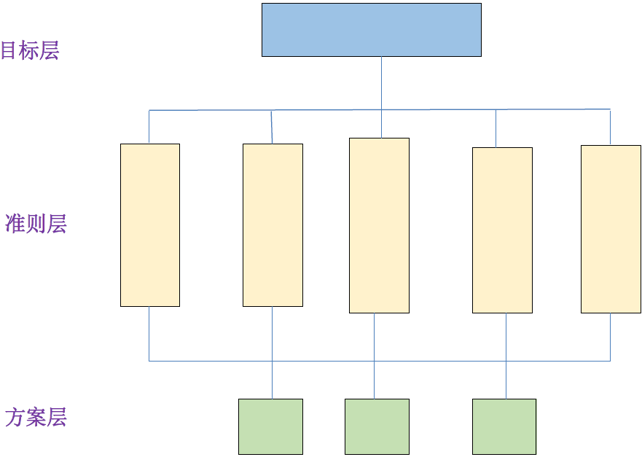
在深入分析实际问题的基础上，将有关的各个因素按照不同属性自上而下地分解成若干层次，同一层的诸因素从属于上一层的因素或对上层因素有影响，同时又支配下一层的因素或受到下层因素的作用。

最上层为目标层，通常只有一个因素，最下层通常为方案或对象层，中间可以有一个或多个层次，通常为准则或指标层。准则层一般 \(5 \sim 7\) 个因素为好，当准则过多时（比如多于 \(9\) 个）应进一步分解出子准则层。

AHP层次结构示意图

2.1.2 构造判断矩阵

构造判断矩阵，这一步是要比较层次结构模型的第二层各个因素对上一层因素影响，从而确定它们对上层因素的影响作用中所占的权重。有时需要理解为下层因素对上层因素的贡献。

设有 \(n\) 个因素 \(x_1,x_2,\cdots,x_n\) 对上一层目标有影响，直接确定它们对目标的影响程度不是很容易，所以每次取两个因素 \(x_i\) 与 \(x_j\) 比较，用 \(a_{ij}\) 表示 \(x_i\) 与 \(x_j\) 对上层目标的影响之比，则 \(A=(a_{ij})_{m\times n}\) 称为判断矩阵或成对比较矩阵。

\[ A=\begin{bmatrix} \dfrac{x_1}{x_1}&\dfrac{x_1}{x_2}&\cdots&\dfrac{x_1}{x_n} \\ \dfrac{x_2}{x_1}&\dfrac{x_2}{x_2}&\cdots&\dfrac{x_2}{x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \dfrac{x_n}{x_1}&\dfrac{x_n}{x_2}&\cdots&\dfrac{x_n}{x_n} \end{bmatrix} \]

判断矩阵主对角线都为 \(1\)，关于主对角线对称的元素互为倒数，所以是正互反矩阵。

Saaty 根据绝大多数人认知事物的心理习惯，建议用\(1 \sim 9\) 及其倒数作为标度来确定 \(a_{ij}\) 的值。

Saaty 发明的 1-9 标度含义
\(i\) 比 \(j\) 强的重要程度 相等 稍强 强 很强 绝对强
\(a_{ij}\) 1 3 5 7 9

其中，2, 4, 6, 8 分别介于 1, 3, 5, 7, 9 对应的重要程度之间。

2.1.3 计算权向量及一致性检验

对于每一个判断矩阵，计算其最大特征根 \(\lambda_{max}\) 及对应特征向量。

再进行一致性检验：利用一致性指标、平均随机一致性指标计算一致性比率。若检验通过，那么归一化特征向量即为权向量；若不通过，需重新构造判断矩阵 .

判断矩阵涉及到的一个关键问题：一致性，这涉及到两两比较的传递性。比如 \(a\) 的重要性是 \(b\) 的 \(2\) 倍，\(b\) 的重要性是 \(c\) 的 \(3\) 倍，则传递过来的 \(a\) 的重要性得是 \(c\) 的 \(6\) 倍，而你对 \(a\) 和 \(c\) 两两比较的重要性不一定是 \(6\) 倍，这就是不一致。

由于判断矩阵构造过程只是在做两两比较，看不到这些传递过来的关系，故不可能做到完全的一致性，所以需要对判断矩阵进行一致性检验：即保证一致性的偏差不能太大。

定义 1 若正互反矩阵 \(A\) 满足： \[ a_{ij}a_{jk}=a_{ik},\quad i,j,k=1,\cdots,n \] 则称 \(A\) 为一致矩阵。

\(n\) 阶一致阵具有如下性质：

  1. 一致阵的唯一非零特征根为 \(n\)

  2. 一致阵的任一列（行）向量都是对应于特征根 \(n\) 的特征向量

因此，判别一个 \(n\) 阶矩阵 \(A\) 是否为一致矩阵，只要计算 \(A\) 的最大特征根 \(\lambda_{max}\) 即可。如果 \(A\) 不是一致矩阵，则可以证明 \(\lambda_{max}>n\)，并且 \(\lambda_{max}\) 越大，不一致程度越严重。

定义 2 设 \(A\) 为 \(n\) 阶判断矩阵，定义一致性指标为： \[ CI = \frac{\lambda_{max}-n}{n-1} \]

当 \(CI = 0\) 时为一致矩阵；\(CI\) 越大，\(A\) 的不一致程度越严重。

前面说了要保证判断矩阵一致性的偏差不能太大，那就需要有个基准，为此，Saaty 采用随机模拟取平均的方法，得到了各阶判断矩阵的一致性的基准：一致性指标 \(RI\)。

不同阶数矩阵的随机一致性指标
矩阵阶数 3 4 5 6 7 8 9 10 11 12 13
\(RI\) 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51 1.54 1.56

有了 \(RI\)，只要一致性指标偏离它的相对偏差不超过一定程度，就可以认为是满足一致性要求。于是，

定义 3 定义一致性比率为： \[ CR = \frac{CI}{RI} \]

规定当 \(CR < 0.1\) 时，\(A\) 的不一致程度在容许范围内，可用其归一化的特征向量作为权重向量，否则需要重新调整判断矩阵 \(A\)。

2.1.4 计算组合权向量与组合一致性检验

为了实现层次分析法的最终目的，需要从上而下逐层进行各层元素对目标层合成权重的计算。

对应单个层次结构的单个判断矩阵必须要满足一致性要求。同样地，各层元素对目标层的合成权重向量是否可以接受，就需要进行综合一致性检验。

注：实际应用中，通常不做整体一致性检验，只保证每个层次结构单独满足一致性检验即可。

2.2 案例：旅游地选择

问题描述：某人要出去旅游，有 \(3\) 个备选旅游地供参考，他准备从景色、费用、居住条件、饮食、旅途共 \(5\) 个因素来考量，最终选择最优的旅游地。

2.2.1 建立层次结构

旅游地选择的层次结构图

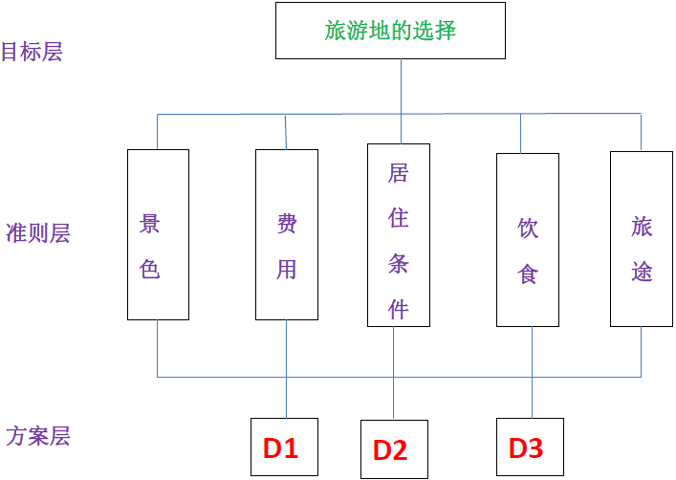
2.2.2 确定判断矩阵

1. 准则层对目标层的判断矩阵

准则层 \(5\) 个因素景色、费用、居住条件、饮食、交通，对目标层旅游地选择的相对重要度，构成 \(1\) 个子结构，需要 \(1\) 个判断矩阵： \[ \begin{bmatrix} 1 & 1/2 & 4 & 3 & 3 \\ 2 & 1 & 7 & 5 & 5 \\ 1/4 & 1/7 & 1 & 1/2 & 1/3 \\ 1/3 & 1/5 & 2 & 1 & 1 \\ 1/3 & 1/5 & 3 & 1 & 1 \end{bmatrix} \] 其中，\(a_{ij}\) 表示 \(x_i\) 与 \(x_j\) 对选择旅游地的相对重要性之比。比如，\(a_{21}=2\) 表示在该人看来，费用 \(x_2\) 是景色 \(x_1\) 的 \(2\) 倍重要。

2. 方案层对准则层的判断矩阵

方案层（\(3\) 个旅游地）对准则层（\(5\) 个因素），构成了 \(5\) 个单独的子结构，需要 \(5\) 个判断矩阵。此时可以理解为 \(3\) 个旅游地分别对每个因素的贡献度（重要度）。

方案层对准则层的各因素的贡献度结构图

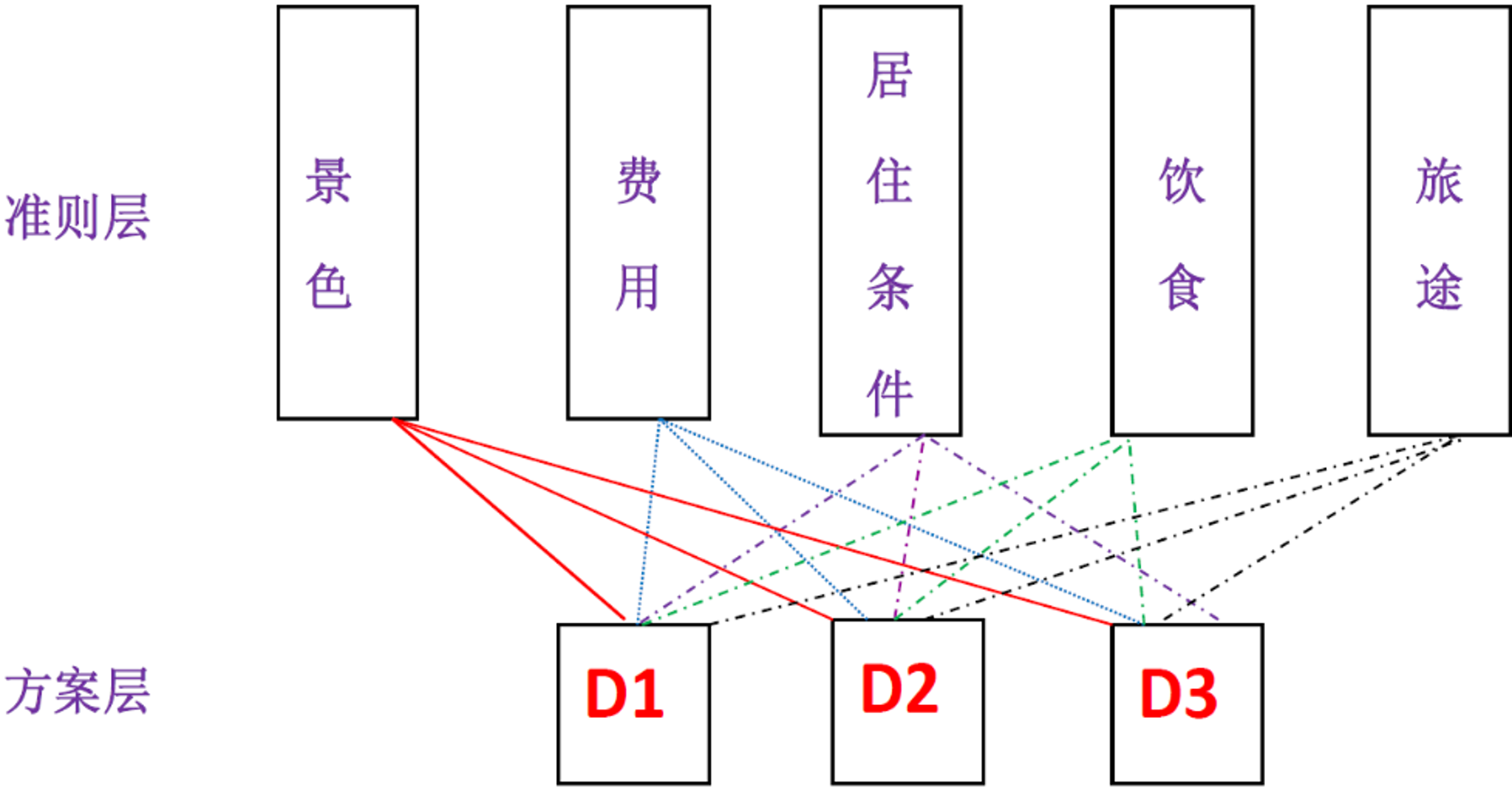
\[ \begin{gathered}B_1=\begin{bmatrix}1&2&5\\1/2&1&2\\1/5&1/2&1\end{bmatrix},\quad B_2=\begin{bmatrix}1&1/3&1/8\\3&1&1/3\\8&3&1\end{bmatrix}\\B_3=\begin{bmatrix}1&1&3\\1&1&3\\1/3&1/3&1\end{bmatrix},\quad B_4=\begin{bmatrix}1&3&4\\1/3&1&1\\1/4&1&1\end{bmatrix},\quad B_5=\begin{bmatrix}1&1&1/4\\1&1&1/4\\4&4&1\end{bmatrix}\end{gathered} \]

2.2.3 基于mathmodels包求解

加载包：

library(tidyverse)
library(mathmodels)

mathmodels 包提供了 AHP() 函数实现一个子结构的层次分析法，只需要提供判断矩阵，就可以计算权重、一致性比率、最大特征值、一致性指标。

本例是层次分析法典型的嵌套层次结构（三个层级，两层判断矩阵），需要对判断矩阵逐层计算，再向上合成。

(1) 第 2 层（下层）

  • 准备判断矩阵：
B1 = matrix(c(1,  2, 5,
              1/2,1, 2,
              1/5,1/2,1), nrow = 3, byrow = TRUE)
B2 = matrix(c(1, 1/3, 1/8,
              3, 1, 1/3,
              8, 3, 1), nrow = 3, byrow = TRUE)
B3 = matrix(c(1, 1, 3,
              1, 1, 3,
              1/3,1/3,1), nrow = 3, byrow = TRUE)
B4 = matrix(c(1, 3, 4,
              1/3,1, 1,
              1/4,1, 1), nrow = 3, byrow = TRUE)
B5 = matrix(c(1, 1, 1/4,
              1, 1, 1/4,
              4, 4, 1), nrow = 3, byrow = TRUE)
  • 批量层次分析法：
res2 = list(B1,B2,B3,B4,B5) |>
  map(AHP)
  • 提取 5 个一致性比率：
map_dbl(res2, "CR")
[1]  4.771648e-03  1.328987e-03 -7.656711e-16  7.933373e-03  0.000000e+00
  • 提取 5 组权重，分别是方案层对准则层每个因素的重要度（贡献度）。按列合并，转化为矩阵：
W2 = map_dfc(res2, "w") |> as.matrix()
W2
          ...1       ...2      ...3      ...4      ...5
[1,] 0.5953790 0.08193475 0.4285714 0.6337079 0.1666667
[2,] 0.2763505 0.23634070 0.4285714 0.1919206 0.1666667
[3,] 0.1282705 0.68172455 0.1428571 0.1743715 0.6666667

该权重矩阵，行代表方案，列代表父级因素，将用于向上合成时的左乘矩阵。注意，若某方案不受某个父级因素支配（无连线），相应位置补 \(0\)。

(2) 第 1 层（上层）

A = matrix(c(1,   1/2, 4, 3,   3,
             2,   1,   7, 5,   5,
             1/4, 1/7, 1, 1/2, 1/3,
             1/3, 1/5, 2, 1,   1,
             1/3, 1/5, 3, 1,   1),
           byrow = TRUE, nrow = 5)
res = AHP(A)
  • 提取一致性比率：
res$CR
[1] 0.01609027
  • 提取权重向量：
W1 = res$w
W1
[1] 0.26360349 0.47583538 0.05381460 0.09806829 0.10867824

(3) 向上合成

  • 即做矩阵乘法：
W2 %*% W1 |> as.vector()
[1] 0.2992545 0.2453040 0.4554415

注：若有更多的层级，继续将新的权重矩阵左乘即可，比如 W3 %*% W2 %*% W1。

该权重向量就是方案层（\(3\) 个旅游地）对目标层（选择旅游地）的权重。其中，第 \(3\) 个权重最大为 \(0.4554\)，所以应该选择第 \(3\) 个旅游地，作为最佳旅游地。