10 模糊综合评价

模糊综合评价法（Fuzzy Comprehensive Evaluation, FCE）是一种基于模糊数学理论的综合评价方法，适用于处理具有模糊性和不确定性的多因素评价问题。该方法通过构建隶属函数，将定性指标转化为定量描述，有效刻画“亦此亦彼”的中间过渡状态，从而克服传统评价方法中“非黑即白”的二值判断局限，使评价结果更加贴近现实情况。

加载包：

library(tidyverse)
library(mathmodels)

10.1 模糊理论

10.1.1 模糊集与隶属度

用数学的眼光看世界，现象分为确定性现象、随机现象、模糊现象（如“今天天气有点冷”，“小伙子很高”等）。模糊理论的基本思想是，用属于程度代替属于或不属于，比如某人属于高个子的程度为 \(0.8\)）。

经典集合语言：

只有两种情况，要么 \(x \in A\)，要么 \(x \notin A\)，用特征函数 \(\chi (\cdot) : A \to \{ 0, 1\}\) 表示： \[ \chi(x) = \left\{ \begin{array}{ll} 1, & x \in A \\ 0, & x \notin A \end{array} \right. \]

模糊集合语言：

用隶属度函数 \(\mu_A(\cdot): A \to [0,1]\) 表示，它确定了 \(X\) 上的一个模糊集 \(A\)。\(\mu_A(x)\) 越接近 \(1\)，表明 \(x\) 属于 \(A\) 的程度越大。

一般用 \(A(x)\) 表示 \(x\) 对模糊集 \(A\) 的隶属度。

注：模糊集与隶属函数，是一一对应的，是同一个事物的两种表示。

例 1 考虑全集：\(\text{周几} = \{\text{周一},\text{周二},\cdots,\text{周日}\}\)。

在经典集语义下说，子集：\(\text{周末} = \{\text{周六}, \, \text{周日}\}\)

周几是否属于周末是完全确定的：是或否
从非周末到周末，是突变过去的

从实际来说，周末并没有严格的界限，周五、周一甚至周四都有一部分也属于周末。这正好符合模糊集语义：

周几是否属于周末，可能是完全属于、部分属于、完全不属于，比如 \(\text{周五属于周末的程度} = 0.8\)
从非周末到周末，是连续变化过去的

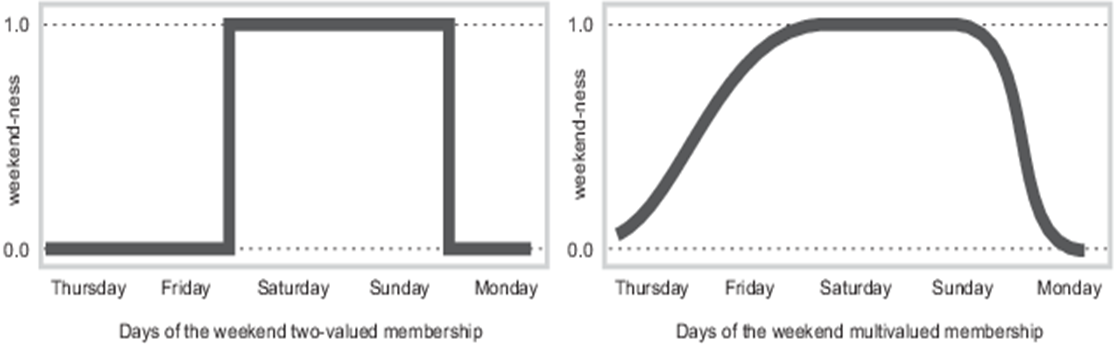
10.1.2 隶属函数

隶属函数 \(\mu_A(x), x \in X\) 将 \(X\) 中每个元映射到 \([0,1]\) 上某个隶属度值。

例如，上面右图就是周几隶属于周末的程度的隶属函数曲线，根据该函数可以计算无论周几的任一时刻属于周末的程度是多少。

隶属函数是任意曲线，其形状可以人为定义，只要简单、方便、快速和高效。准确地确定隶属函数是定量刻化模糊概念的基础，也是利用模糊方法解决各种实际问题的关键。

常用隶属函数确定方法：模糊统计法，主观/专家经验法，二元对比排序法，拟合模糊分布法，最小模糊度法。

10.1.2.1 模糊统计法

模糊统计法，是基于评委评语/打分的数据统计，这是 tidyverse 最擅长的。

1. 从评委打分/评语数据到隶属矩阵

例如，模糊综合评价衣服的评语集为：“差”、“一般”、“好”。评委直接给出若干评价对象（衣服）各指标的评语，当然评委也可以是打分，根据分数阈值离散化到各评语。

这样的数据，不需要隶属函数，做分组统计就能得到隶属向量。

比如，某件衣服，对于色彩，经过统计发现：\(80\%\) 的评委认为是 “好”，\(10\%\) 的评委认为是”一般”，\(10\%\) 的评委认为是”差”。

则该件衣服的色彩隶属于评语集每个评语：“好”、“一般”、“差”的隶属度，即隶属向量为：\([0.8, 0.1, 0.1]\)

同理，处理其他指标：做工、品牌、款式。

下面随机生成了一个数据作为演示，包含 \(10\) 个评委对 \(3\) 件衣服上述 \(4\) 个指标的打分：

set.seed(1)
df = matrix(sample(30:100, 120, replace = TRUE), ncol = 10) |> 
  as_tibble(.name_repair = "universal") |> 
  set_names(str_c("评委", 1:10)) |> 
  mutate(ID = rep(1:3, each = 4), 
         指标 = rep(c("颜色","做工","品牌","款式"), 3), .before = 1)

第一步，先宽变长变整洁，根据阈值，比如 \([60, 75]\) 离散化为评语：

df = df |>
  pivot_longer(-(1:2), names_to = "评委", values_to = "打分") |>
  mutate(评语 = case_when(打分 < 60 ~ "差",
                          打分 < 75 ~ "一般",
                          .default = "好"),
         评语 = factor(评语, levels = c("差","一般","好")))
df

# A tibble: 120 × 5
      ID 指标  评委    打分 评语 
   <int> <chr> <chr>  <int> <fct>
 1     1 颜色  评委1     97 好   
 2     1 颜色  评委2     66 一般 
 3     1 颜色  评委3     99 好   
 4     1 颜色  评委4     31 差   
 5     1 颜色  评委5     42 差   
 6     1 颜色  评委6     80 好   
 7     1 颜色  评委7     77 好   
 8     1 颜色  评委8     66 一般 
 9     1 颜色  评委9     36 差   
10     1 颜色  评委10    46 差   
# ℹ 110 more rows

第二步，数据统计：分组汇总评语频数，分组计算评语百分比

df = df |>
  count(ID, 指标, 评语) |>
  mutate(p = n / sum(n), .by = c(ID, 指标))
df

# A tibble: 35 × 5
      ID 指标  评语      n     p
   <int> <chr> <fct> <int> <dbl>
 1     1 做工  差        2   0.2
 2     1 做工  一般      7   0.7
 3     1 做工  好        1   0.1
 4     1 品牌  差        6   0.6
 5     1 品牌  一般      3   0.3
 6     1 品牌  好        1   0.1
 7     1 款式  差        3   0.3
 8     1 款式  一般      3   0.3
 9     1 款式  好        4   0.4
10     1 颜色  差        4   0.4
# ℹ 25 more rows

第三步，整理结果得到每件衣服的隶属矩阵

第二步已经计算出了所有隶属向量中的元素，只不过是堆在了一列 p 当中。每件衣服的取出来，每个评语的占一列，就是隶属矩阵。需要做的就是：按衣服切分 + 长变宽。

先把一件衣服做长变宽，写成函数：

f = function(data) {
  data |>
    pivot_wider(id_cols = 评语, names_from = 指标, values_from = p) |>
    select(-评语)
}

再按衣服切分数据，批量地做长变宽：

split(df, df$ID) |>
  map(f)

$`1`
# A tibble: 3 × 4
   做工  品牌  款式  颜色
  <dbl> <dbl> <dbl> <dbl>
1   0.2   0.6   0.3   0.4
2   0.7   0.3   0.3   0.2
3   0.1   0.1   0.4   0.4

$`2`
# A tibble: 3 × 4
   做工  品牌  款式  颜色
  <dbl> <dbl> <dbl> <dbl>
1   0.3   0.4   0.3  NA  
2   0.3   0.3   0.4   0.5
3   0.4   0.3   0.3   0.5

$`3`
# A tibble: 3 × 4
   做工  品牌  款式  颜色
  <dbl> <dbl> <dbl> <dbl>
1   0.4   0.5   0.5   0.6
2   0.1   0.1   0.3   0.1
3   0.5   0.4   0.2   0.3

2. 从评委区间数据到隶属函数

这是模糊理论中理解隶属函数的经典示例，根据关于“青年人”年龄区间调查表，确定“青年人”的隶属函数。

该表记录了 129 位专家关于“青年人”年龄区间的调查结果。

df = readxl::read_excel("data/youth.xlsx", 
                        col_names = FALSE) |> 
  set_names(str_c("g", 1:13))
df

# A tibble: 10 × 13
   g1    g2    g3    g4    g5    g6    g7    g8    g9    g10   g11   g12   g13  
   <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr>
 1 18−25 18−30 17−30 20−35 15−28 18−25 18−35 19−28 17−30 16−30 15−28 15−25 16−28
 2 18−30 18−25 18−28 17−30 15−30 18−30 18−35 15−25 17−25 17−30 18−35 18−25 18−30
 3 16−28 18−30 18−35 15−30 18−35 15−28 15−25 16−32 18−30 18−35 17−30 18−35 16−28
 4 20−30 16−30 18−35 18−35 18−29 17−28 18−35 18−35 18−25 18−30 16−28 17−27 15−26
 5 16−35 18−35 15−25 15−27 18−35 16−30 14−25 18−25 18−30 20−30 18−28 18−30 15−30
 6 18−28 18−25 16−25 20−30 18−35 18−30 18−30 16−28 17−25 16−30 18−30 15−25 18−35
 7 18−30 18−28 18−26 16−35 16−28 16−25 15−35 17−30 15−25 16−35 15−30 18−30 15−25
 8 16−30 16−30 15−28 15−36 15−25 17−28 18−30 16−25 18−30 17−25 18−29 17−29 15−30
 9 17−30 16−30 16−35 15−30 14−25 18−35 16−30 18−30 18−35 16−28 18−25 18−30 18−28
10 18−35 16−24 18−30 17−30 15−30 18−35 18−25 18−30 15−30 15−30 17−30 18−30 <NA>

第一步，数据处理：宽变长（忽略缺失）、分割列（转化数值）

df = df |>
  pivot_longer(everything(), names_to = "g", values_to = "x", 
               values_drop_na = TRUE) |>
  separate(x, c("x1", "x2"), sep = "−", convert = TRUE) |>
  select(-g)
df

# A tibble: 129 × 2
      x1    x2
   <int> <int>
 1    18    25
 2    18    30
 3    17    30
 4    20    35
 5    15    28
 6    18    25
 7    18    35
 8    19    28
 9    17    30
10    16    30
# ℹ 119 more rows

这样就得到了，每位专家认为的属于“青年人”的最小年龄和最大年龄。

第二步，构建隶属函数

“青年人”的隶属函数，就是包含年龄 x 的年龄区间（最小年龄和最大年龄之间）的占比：

mf = function(x) {
  summarise(df, p = mean(x1 <= x & x <= x2)) |>
    pull(p)
}

有一个或多个年龄，都能计算隶属度：

ages = c(25, 16.5, 20, 43)
map_dbl(ages, mf)

[1] 0.9922481 0.3953488 1.0000000 0.0000000

可视化该“青年人”隶属函数：

tibble(年龄 = 10:40, 隶属度 = map_dbl(年龄, mf)) |>
  ggplot(aes(年龄, 隶属度)) +
  geom_line() +
  geom_point() +
  geom_segment(aes(xend = 年龄, yend = 0), alpha = 0.2) +
  theme_minimal()

10.1.2.2 主观/专家经验法

主观/专家经验法，是由领域专家根据经验或直观判断直接设定隶属函数的形式和参数，无需依赖数据统计或复杂计算。

比如，常用的三角隶属函数、梯形隶属函数、高斯隶属函数：

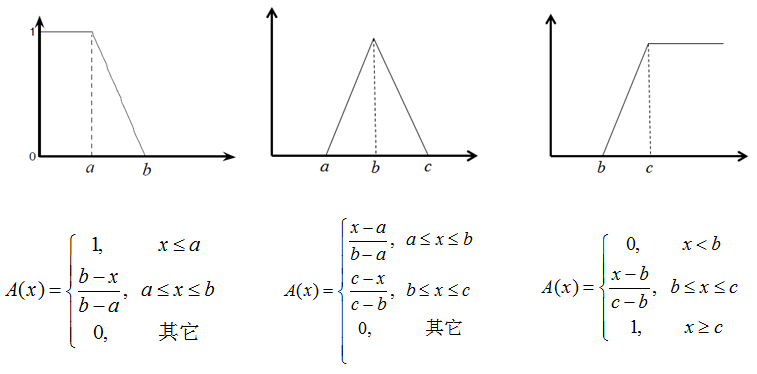
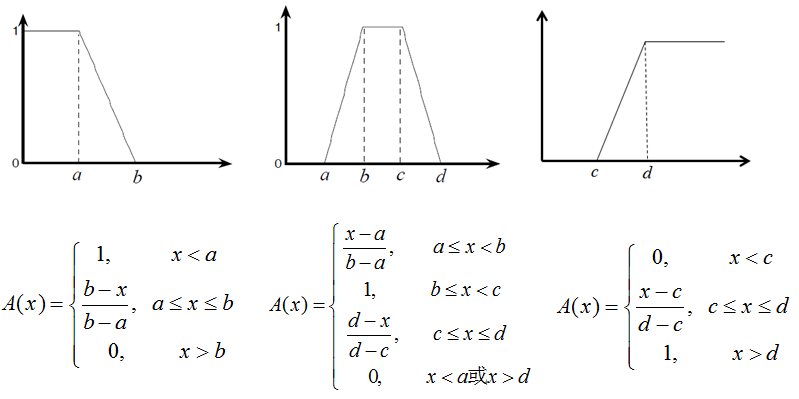
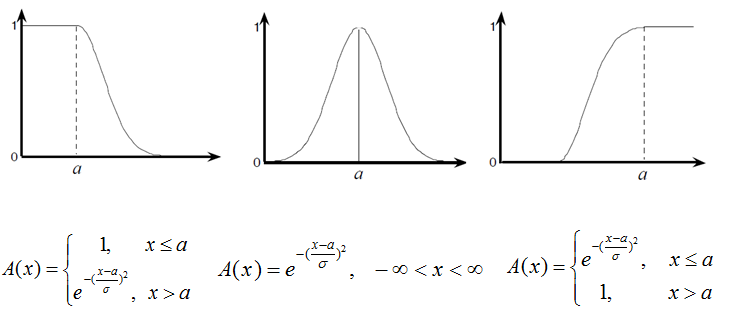
隶属度函数的理解：以梯形隶属度函数为例，比如某指标值最优区间是 \([5,10]\)，则落在该区间内的该指标值，我们认为都是“最优”的，但 \(4.7\) 呢？我们不希望从 \(5\) 直接就到不是”最优”，而是让它们有一个自然的过度，比如取 \([4,5]\) 和 \([10,11]\) 线性过度到不是”最优”，那么关于 \(4.7\) 这个点，有 \(\dfrac{4.7-4}{5-4}=0.7\)，即 \(4.7\) 隶属于最优区间 \([5,10]\) 的程度是 \(0.7\)。

另外，还有双高斯隶属函数、广义贝尔隶属函数、Sigmoid 隶属函数族（单 Sigmoid、两 Sigmoid 之差、两 Sigmoid 之积）、多项式隶属函数族（分别形如\(Z,\bar{\pi},S\)）。

mathmodels 包提供了上述所有隶属函数的实现，以及可视化隶属函数的函数：

tri_mf(x, params)
trap_mf(x, params)
gauss_mf(x, params)
gbell_mf(x, params)
gauss2mf(x, params)
sigmoid_mf(x, params)
dsigmoid_mf(x, params)
psigmoid_mf(x, params)
z_mf(x, params)
pi_mf(x, params)
s_mf(x, params)
plot_mf(mf, xlim = c(0, 10), main = NULL)

其中，x 为数值向量，params 为各隶属函数相应参数值向量，返回与 x 同样长度的隶属度值。

以梯形隶属函数为例，包含 \(4\) 个参数，比如取 1,5,7,8，计算 1:10 的隶属度值：

x = 1:10
trap_mf(x, params = c(1, 5, 7, 8))

 [1] 0.00 0.25 0.50 0.75 1.00 1.00 1.00 0.00 0.00 0.00

可视化该梯形隶属函数：

f = \(x) trap_mf(x, c(1, 5, 7, 8))
plot_mf(f, xlim = c(0,10), main = "梯形隶属函数")

10.1.3 `compute_mf()` 函数

将单个指标值转化为属于各评语的隶属向量，是模糊综合评价计算隶属矩阵最核心的、大量重复使用的计算步。而非常常见且合理的做法，就是三角+梯形隶属函数法，或叫做分段线性隶属函数法。

mathmodels 包提供了 compute_mf() 函数，实现基于三角隶属（两端是半梯形）将单个指标值转化为属于各评语的隶属向量，基本语法为：

compute_mf(x, thresholds)

x 为单个指标值；
thresholds 为指标值划分到各评语的中间界限构成的向量（长度至少为 \(2\)）
返回 mv 为隶属向量，对应单个评价对象的单个指标值。

用法示例

举个例子，大气污染物评价，其中 SO2 的四个等级阈值为：

污染物	一级	二级	三级	四级
SO2	0.05	0.15	0.25	0.50

这表示：\(≤ 0.05\) 是一级（\(100\%\) 隶属），\(0.15\) 是二级，\(0.25\) 是三级，\(≥ 0.50\) 是四级；中间区间线性从 \(1\) 减到 \(0\)，比如 \([0.05, 0.15]\) 一级的隶属度是从 \(1\) 线性降到 \(0\)，二级隶属是从 \(0\) 线性升到 \(1\)，其他类似。

结合函数图形来理解更加直观。为了便于可视化演示，顺便提供了 compute_mf_funs 函数返回所有隶属函数，再用 plot_mf 函数做可视化：

th = c(0.05, 0.15, 0.25, 0.50)
mfs = compute_mf_funs(th)
plots = lapply(mfs, \(x) plot_mf(x, xlim = c(0, 0.6))) 
gridExtra::grid.arrange(grobs = plots, nrow = 2)

分别是一级、二级、三级、四级的隶属函数，形状依次为右半梯形、三角形、三角形、左半梯形。以右上“二级”隶属函数为例，0.15 处为 1，区间 [0.05, 0.15] 上线性增长到 1。

比如，某天的 SO2 含量为 0.07，转化为隶属向量：

compute_mf(0.07, th)        # 计算隶属向量

[1] 0.8 0.2 0.0 0.0

这 4 个值，就是将 0.07 分别代入上述 4 个隶属函数得到的函数值构成。这表明，0.07 隶属于“一级”的程度是 0.8，隶属于“二级”的程度是 0.2，隶属于后两级的程度都是 0。

10.1.4 模糊运算

10.1.4.1 模糊逻辑运算

经典集特征函数值只取 \(0\) 和 \(1\)，标准布尔逻辑运算：与、或、非

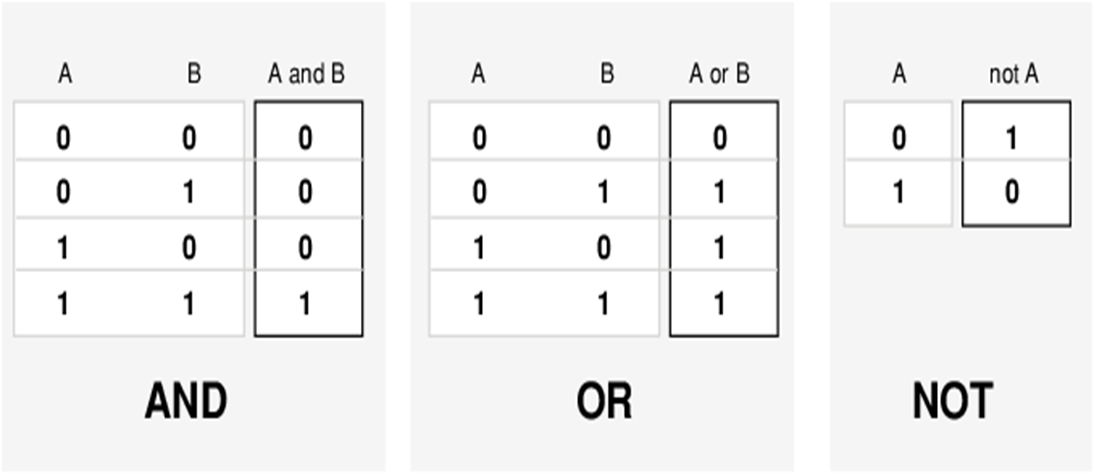
换个写法：与 就是取 \(\min\)，或 就是取 \(\max\)，非就是做 \(1-x\)

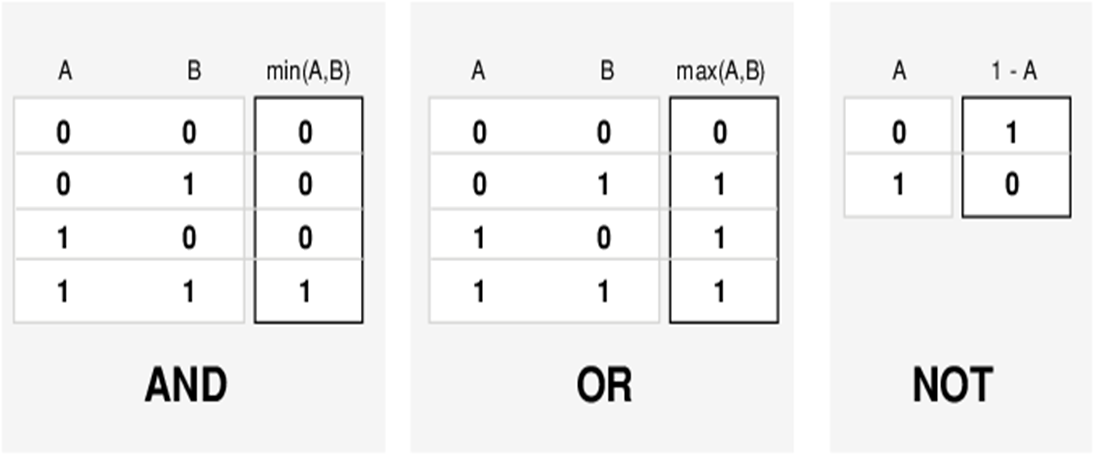
从经典集的布尔运算到模糊集的模糊运算，模糊集的隶属函数取值是 \([0,1]\)。

模糊集与隶属函数（曲线）一一对应，所以，很自然地，模糊集的逻辑运算，就等同于隶属函数（曲线）的逻辑运算（取 \(\min\)、取 \(\max\)、做 \(1-x\)）。

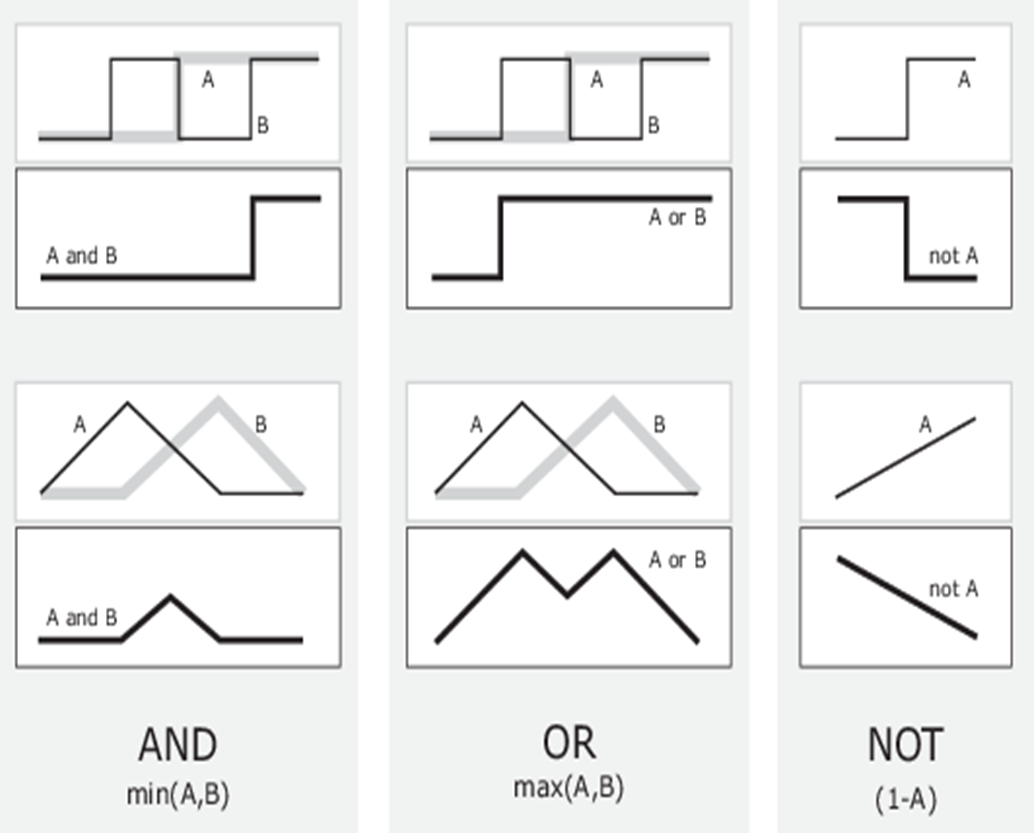
10.1.4.2 模糊合成

设 \(R=(r_{ij})_{m\times n}\) 为矩阵，若满足 \(0\leq r_{ij}\leq 1\)，称为模糊矩阵，若 \(r_{ij}\) 只取 \(0\)或 \(1\) 时，称为布尔矩阵。

模糊综合评价涉及模糊变换，即将模糊评价矩阵作用到向量，得到新向量： \[ B_{m\times1}=R_{m\times n}\circ A_{n\times1} \] 其中，\(\circ\) 为模糊合成算子，记 \(A=[a_1,\cdots,a_m]^T, \, B=[b_1,\cdots,b_m]^T\)。

模糊变换根据目的不同，可以选择不同的模糊合成算子：

(1) 取小取大，主因素决定型

\[ b_j = \max_i\big\{\min \{a_i,r_{ij}\}\big\},\quad j=1,\cdots,m \] 通常用的算子，其评判结果只取决于在总评价中起主要作用的那个因素，其余因素均不影响评判结果，比较适用于单项评判最优就能作为综合评判最优的情况。

(2) 乘积最大，主因素突出型

\[ b_j=\max_i \{a_i\cdot r_{ij} \},\quad j=1,\cdots,m \]

与取小取大相近，但更精细些，不仅突出了主要因素，也兼顾了其他因素。此模型适用于模型失效（不可区别），需要“加细”的情况。

(3) 乘加，加权平均型

\[ b_j=\sum_{i=1}^n a_i \cdot r_{ij}, \quad j=1,\cdots,m \] 该算子依权重的大小对所有因素均衡兼顾，比较适用于求总和最大的情形。

(4) 取小上界和型

\[ b_j = \min\Big\{1,\sum_{i=1}^n \min \{a_i,r_{ij} \}\Big\}, \quad j=1,\cdots,m \] 在使用此算子时，需要注意：各个 \(a_i\) 不能取得偏大，否则可能出现 \(b_j\) 均等于 \(1\) 的情形；各个 \(a_i\) 也不能取得太小，否则可能出现 \(b_j\) 均等于各个 \(a_i\) 之和的情形，这将使单因素评判的有关信息丢失。

(5) 均衡平均型

\[ b_j = \sum_{i=1}^n \Big(a_i \wedge \frac{r_{ij}}{r_0}\Big), \quad j=1,\cdots,m \] \(r_{0}=\sum\limits_{k=1}^{m}r_{kj}\)，该算子实际上先对模糊评价矩阵 \(R\) 中的列向量做了归一化处理, 适用于 \(R\) 中元素偏大或偏小的情形。

mathmodels 包提供了 fuzzy_eval() 函数实现模糊合成，基本语法为：

fuzzy_eval(w, R, type)

w 为各因素的权重向量，R 为模糊评价矩阵，type 可选上述 \(5\) 种模糊合成算子：\(1 \sim 5\)。

10.2 模糊综合评价算法步骤

(1) 确定因素集及权重向量

设某评价对象的评价因素有 \(n\) 个，记作 \(U=\{u_1,\cdots,u_n\}\)，称为因素集。由于各种因素所处地位和作用的不同，考虑用权重向量来衡量，实际中该权重向量可以借助主客观赋权法来得到。

例如，某人要购买一件衣服，她要考虑 4 个因素： \[ u_1=\text{色彩},\quad u_2 =\text{做工}, \quad u_3=\text{品牌},\quad u_4=\text{款式} \]

4 个因素在评价过程中的权重向量为 \(w = [0.3,0.3,0.3,0.1]^T\)。

(2) 确定评语集

设所有可能的评语有 \(m\) 个，记为 \(V=\{v_1,⋯,v_m\}\)，称为评语集。

例如，对衣服的评语集为 \[ v_1=\text{好}, \quad v_2=\text{一般}, \quad v_3=\text{差} \]

(3) 建立模糊评价矩阵

先对该事物的每个因素隶属于各个评语的程度进行评价（评委打分或经验隶属函数）。

例如，某件衣服，对于”色彩”，\(80\%\) 的评委认为是“好”，\(10\%\) 的评委认为是”一般”，\(10\%\) 的评委认为是”差”。

则该件衣服因素 1：“色彩”隶属于评语集每个评语：“好”、“一般”、“差”的隶属度为：\(r_1=[0.8,0.1,0.1]^T\)；

同样，因素 2：“做工”隶属于每个评语：“好”、“一般”、“差”的隶属度为：\(r_2=[0.7,0.2,0.1]^T\)；

因素 3：“品牌” 隶属于每个评语：“好”、“一般”、“差”的隶属度为：\(r_3=[0.6,0.2,0.2]^T\)；

因素 4：“款式” 隶属于每个评语：“好”、“一般”、“差”的隶属度为：\(r_{4}=[0.7,0.1,0.2]^{T}\)。

于是，得到模糊评价矩阵： \[ R = [r_1,r_2,r_3,r_4] = \begin{bmatrix} 0.8&0.7&0.6&0.7\\ 0.1&0.2&0.2&0.1\\ 0.1&0.1&0.2&0.2 \end{bmatrix} \]

(4) 做模糊综合合成

基于合适的模糊合成算子，比如选 3 加权平均型，做模糊合成得到模糊评价向量：\(\mu=R\circ w\)，一般对 \(\mu\) 进行归一化处理。

这里的 \(R\) 是分别的、单独的评价（隶属程度），再综合各因素占的权重 \(w\)，所以叫做模糊综合评价。

w = c(0.3, 0.3, 0.3, 0.1)
R = matrix(c(0.8, 0.7, 0.6, 0.7,
             0.1, 0.2, 0.2, 0.1,
             0.1, 0.1, 0.2, 0.2), nrow = 3, byrow = TRUE)
mu = fuzzy_eval(w, R, 3)
mu

[1] 0.70 0.16 0.14

(5) 去模糊化得到最终评价

模糊评价向量 \(\mu\) 是这件衣服对各评语：“好”、“一般”、“差”的隶属度，要得到最终评语或评分，还需要做一步去模糊化。

mathmodels 包，提供了 defuzzify() 函数，实现对模糊评价向量去模糊化，基本语法为：

defuzzify(mu, scores, method = "weighted_average")

mu 为模糊评价向量；
scores 为各评语的量化分数；
method 选择去模糊化方法，可选 "max_membership"：最大隶属度法（隶属度最大值对应评语的量化分数）、"weighted_average"：加权平均法（默认，隶属度值与各评语量化分数做加权求和）、"centroid"：重心法。

注：对于归一化的模糊评价隶属向量，加权平均法与重心法结果是相同的。

scores = c(90, 75, 50)
defuzzify(mu, scores, method = "max_membership")       # 最大隶属度法

[1] 90

defuzzify(mu, scores)                                  # 加权平均法

[1] 82

10.3 案例：耕作方案的模糊综合评价

某平原产粮区进行耕作制度改革，制定了甲（三种三收）、乙（两茬平作）、丙（两年三熟）3 种方案。主要评价指标选取 5 项：粮食亩产量、农产品质量、每亩用工量、每亩纯收入、生态环境影响。根据当地实际情况，这 5 个因素的权重分别为 \(0.2, 0.1, 0.15, 0.3, 0.25\)，其评价等级如表 1 所示：

耕作方案评价指标数据的等级划分
分数	亩产量/kg	产品质量/级	亩用工量/工日	亩纯收入/元	生态环境影响/级
优	550 以上	1	20 以下	130 以上	1
良	450-550	2	20-40	90-130	2
中	350-450	3	40-60	50-90	3
差	350 以下	4	60 以上	50 以下	4

经过调查并应用各种参数进行计算预测，发现 3 种方案的 5 项指标可达到表 2 中的数值：

三种耕作方案的指标数据
方案	亩产量/kg	产品质量/级	亩用工量/工日	亩纯收入/元	生态环境影响/级
甲	592.5	3	55	72	4
乙	529	2	38	105	3
丙	412	1	32	85	2

问究竟应该选择哪种方案？

模糊综合评价，超级简洁、可以随便替换成自己数据的通用流程如下：

compute_mf 函数是根据指标阈值和单个指标值，计算隶属向量；
批量调用compute_mf 函数，对一个评价对象（耕作方案）的所有指标值和相应指标阈值，都算一遍再合并，就计算出隶属矩阵；
隶属矩阵和指标权重向量做模糊综合合成（fuzzy_eval 函数），就得到模糊综合评价结果向量，再去模糊化（defuzzify 函数）到最终评价分数；
再对每个评价对象重复上述过程。

下面具体求解。

10.3.1 准备评价对象数据（表2）

df = tibble(product = c(592.5, 529, 412), quality = 3:1, 
            labor = c(55, 38, 32), 
            income = c(72, 105, 85), ecology = 4:2)
df

# A tibble: 3 × 5
  product quality labor income ecology
    <dbl>   <int> <dbl>  <dbl>   <int>
1    592.       3    55     72       4
2    529        2    38    105       3
3    412        1    32     85       2

数据预处理

注意，产品质量、亩用工量、生态环境影响是负向指标，需要转化为正向。应该从固定不变的阈值考虑（而不是可变的具体方案指标值），采用最大值 + 平移值做差方式。比如，1、2、3、4 要变成 4、3、2、1，需要的变换是 \(5 - x\)；而 20、40、60 要变成 60、40、20，需要的变换是 \(80 - x\)

df = df |> 
  mutate(across(c(2,5), \(x) 5 - x), labor = 80 - labor)
df

# A tibble: 3 × 5
  product quality labor income ecology
    <dbl>   <dbl> <dbl>  <dbl>   <dbl>
1    592.       2    25     72       1
2    529        3    42    105       2
3    412        4    48     85       3

10.3.2 准备阈值数据（从表1提炼，用于计算隶属向量）

评语集是分数列，对应到优良中差：3（优）、2（良）、1（中）、0（差）。注意，共有 4 个评语，需要 4 个阈值（同示例）。产品质量和生态环境是 \(1, 2, 3, 4\)（可以直接用），其他三个，比如亩产量只提供了 3 个阈值：\(350, 450, 550\)，显然在前面补一个 \(0\) 是合理的。

th_mat = tibble(
  th1 = c(0, 350, 450, 550),            # 亩产量 
  th2 = 1:4,                            # 产品质量
  th3 = seq(0,60,20),                   # 亩用工量
  th4 = c(0, 50, 90, 130),              # 亩收入
  th5 = 1:4)                            # 生态环境影响

10.3.3 批量模糊综合评价

本例只有 3 个评价对象，当然可以一个一个地分别计算。

为了通用于任意多个评价对象，把对一个评价对象做模糊综合评价的写成函数：

eval_one = function(x, type = 3, method = "max_membership") {
  # x为一个评价对象(提取df的某一行, 转化为向量)
  R = map2_dfc(x, th_mat, compute_mf) 
  mu = fuzzy_eval(w, R, type)               # 默认对结果归一化
  s = defuzzify(mu, scores, method)
  list(s = s, mu = mu, R = R)
}

其中，type 选择模糊合成的方法，可选 1：取小取大（主因素决定）、2：乘积最大（主因素突出）、3：乘加（加权平均）、4：取小上界和、5：均衡平均。 method 选择去模糊化方法，可选 "max_membership"：最大隶属度法、"weighted_average"：加权平均法、"centroid"：重心法。