11 数据包络分析
数据包络分析(DEA),是一种基于线性规划的非参数评估方法。它通过构建相对效率评价模型,对多个具有多投入、多产出特征的决策单元(DMU)进行绩效评估和效率排序。DEA 的核心优势在于,它能够根据每个决策单元自身的投入和产出数据,自动优化其权重配置。这种方法无需事先设定固定的权重,从而能够更客观、真实地识别出对每个决策单元最有利的评价标准,准确反映其个体特征和实际运行效率。
DEA 已被广泛应用于生产管理、行政绩效评估等诸多领域。它不仅可以用于评估不同方案的相对有效性,例如投资项目的效益比较,还可以在决策前进行效果预测,或在政策实施后评估其成效。通过 DEA 的辅助,决策者能够更科学地制定策略,提升管理和决策的精准性。
DEA 优点:
- 多指标处理能力:DEA 擅长处理多输入和多输出指标的综合评价问题,适用于复杂系统的效率评估。
- 无需无量纲化:DEA 不对数据进行无量纲化处理,因为其效率指标的计算与输入输出数据的量纲无关。
- 客观性强:DEA 无需事先设定权重,而是根据实际数据计算最优权重,减少了主观因素的干扰,提高了评估的客观性。
- 灵活的关系建模:DEA 假定输入和输出之间存在某种联系,但不需要明确表达这种关系的具体形式,从而增加了模型的灵活性。
DEA 缺点:
- 数据依赖性:DEA 的效率评估结果依赖于所收集的数据,最优效率仅在当前样本范围内有效。
- 技术有效单元的局限性:DEA 无法对技术有效单元进行进一步比较,且未考虑系统中的随机因素,可能导致在存在异常点时评估结果失真。
11.1 DEA 相关概念
设有 \(n\) 个部门或决策单元 (DMU),每个决策单元有 \(m\) 个输入变量和 \(q\) 个输出变量: \[ \begin{array}{ccccccccc} &&& m~\text{个投入} &&&& q~\text{个产出} \\ \text{DMU/指标}~ & ~x_1 & x_2 & \cdots & x_m~ & ~y_1 & y_2 & \cdots & y_q \\ 1~ & ~x_{11} & x_{12} & \cdots & x_{1m}~ & ~y_{11} & y_{12} & \cdots & y_{1q} \\ 2~ & ~x_{21} & x_{22} & \cdots & x_{2m}~ & ~y_{21} & y_{22} & \cdots & y_{2q} \\ \vdots~ & ~\vdots & \vdots & \ddots & \vdots~ & ~\vdots & \vdots & \ddots & \vdots \\ n~ & ~x_{n1} & x_{n2} & \cdots & x_{nm}~ & ~y_{n1} & y_{n2} & \cdots & y_{nq} \\ & \uparrow & \uparrow & \cdots & \uparrow~ & ~\uparrow & \uparrow & \cdots & \uparrow \\ \text{权重}~ & ~v_1 & v_2 & \cdots & v_m~ & ~ u_1 & u_2 & \cdots & u_m \end{array} \] 用 \(i=1,\cdots,n\) 表示决策单元的索引;\(j=1,\cdots,m\) 表示投入指标的索引; \(r=1,\cdots,q\) 表示产出指标的索引。
改用向量形式表示,记 \[ X_i=[x_{i1},x_{i2},\cdots,x_{im}],\quad Y_i=[y_{i1},y_{i2},\cdots,y_{iq}],\quad i=1,\cdots,n \] \[ v = [\nu_1,\cdots,\nu_m],\quad u =[u_1,\cdots,u_q] \] 则 \(X_i,Y_i\) 分别为第 \(i\) 个决策单元的输入向量、输出向量;\(v,u\) 分别为输入权重、输出权重。
DEA 评价的是技术效率,是指一个决策单元的生产过程达到本行业技术水平的程度。一般来说,技术效率可以使用产出和投入的比例衡量,但这种衡量方式一般仅适用于单投入单产出的情形。对于 \(m\) 个投入和 \(q\) 个产出,则第 \(k\) 个决策单元的技术效率,可以用加权方式确定其综合的投入产出来刻画: \[ h_k=\frac{\sum_{r=1}^qu_ry_{kr}}{\sum_{j=1}^m\nu_jx_{kj}} \] 关于投入与产出导向:
在径向 DEA 中,无效率往往是通过投入和产出的等比例变化定义的,因此既可以在给定投入的情况下最大化产出(产出导向),也可以在给定产出的情况下最小化投入(投入导向)。
对于不同的规模收益假设,不同导向的效率分析结果可能存在一定差异。对于规模收益不变的模型(CRS),两种导向的效率结果是一样的;而对于可变规模收益模型(VRS)中,二者是不同的。
在实践中,投入和产出导向的选择没有明确的要求,实际选择时最好是根据具体生产活动的实际,看是投入倾向于固定不变还是产出倾向于固定不变。
DEA 模型的编程实现:
R 语言有 deaR 包等可以实现 DEA 模型。
手动编程实现的话,因为本质上就是求解线性规划问题,在模型公式确定后,其编程过程可遵循如下步骤:
- 确定参数列向量;
- 将模型表示为线性规划标准形式;
- 改成用矩阵语言表示,梳理出各矩阵、向量;
- 调用线性规划求解器进行求解。
11.2 常用 DEA 模型
11.2.1 CCR模型 (规模收益不变假设下的径向 DEA 模型)
(1) 投入导向的 CCR 模型
在给定投入的条件下最大化产出。将前面加权方式的投入产出技术效率,再将其范围限制为 \([0,1]\),则得到投入导向的 CCR 模型:对每个决策单元 \(k\), \[ \begin{aligned} &\max\frac{\sum_{r=1}^qu_ry_{kr}}{\sum_{j=1}^m v_jx_{kj}}\\ \mathbf{s.t.~~}&\frac{\sum_{r=1}^qu_ry_{kr}}{\sum_{j=1}^m v_jx_{kj}}\leq1\\ & v_j\geq0,u_r\geq0,\quad j=1,\cdots,m;\;r=1,\cdots q \end{aligned} \]
通过 Charnes-Cooper 变换线性化转化为线性规划:对每个决策单元 \(k\), \[ \begin{aligned}&\max\sum_{r=1}^q\mu_ry_{kr}\\\mathbf{s.t.~~}&\sum_{r=1}^q\mu_ry_{kr}-\sum_{j=1}^m \nu_jx_{kj}\leq0\\&\sum_{j=1}^m \nu_jx_{kj}=1\\&\mu_r\geq0, \nu_j\geq0,\quad j=1,\cdots,m; \; r=1,\cdots q\end{aligned} \]
上述问题的对偶形式为(对偶模型的决策变量中包含效率值): 对每个决策单元 \(k\) \[ \begin{aligned}&\min\theta\\\mathrm{s.t.~~}&\sum_{i=1}^n\lambda_ix_{ij}\leq\theta x_{kj}\\&\sum_{i=1}^n\lambda_iy_{ir}\geq y_{kr}\\&\lambda_i\geq0,\quad j=1,\cdots,m;\;r=1,\cdots q\end{aligned} \]
该对偶模型中,\(\lambda_i,i=1,\cdots,n\) 表示 DMU 的线性组合系数,参数 \(\theta\) 的最优解 \(\theta^*\) 即为效率值,其范围落在 \([0,1]\)。
该模型的含义相当于用加权方法构造出一个不存在的 DMU,其投入不大于待评价的 DMU,产出不小于待评价的 DMU,即 \[ x=\sum_{i=1}^n\lambda_ix_{ij},\quad y=\sum_{i=1}^n\lambda_ix_{ir} \]
为了便于求解,进一步改写为矩阵形式: \[ \begin{aligned} &\min\left[0,\cdots,0,1\right]\left[\lambda_1,\cdots,\lambda_n,\theta\right]^T\\ \mathbf{s.t.}&\begin{bmatrix}x_{11}&x_{21}&\cdots&x_{n1}&-x_{i1}\\x_{12}&x_{22}&\cdots&x_{n2}&-x_{i2}\\ \vdots&\vdots&\ddots&\vdots&\vdots\\ x_{1m}&x_{2m}&\cdots&x_{nm}&-x_{im}\end{bmatrix}\begin{bmatrix}\lambda_1\\ \vdots\\ \lambda_n\\ \theta\end{bmatrix}\leqslant\begin{bmatrix}0\\ 0\\ \vdots\\ 0\end{bmatrix}\\ &\begin{bmatrix}-y_{11}&-y_{21}&\cdots&-y_{n1}&0\\ -y_{12}&-y_{22}&\cdots&-y_{n2}&0\\ \vdots&\vdots&\ddots&\vdots&\vdots\\ -y_{1q}&-y_{2q}&\cdots&-y_{nq}&0 \end{bmatrix} \begin{bmatrix} \lambda_1\\ \vdots\\ \lambda_n\\ \theta \end{bmatrix} \leqslant\begin{bmatrix}-y_{i1}\\ -y_{i2}\\ \vdots\\ -y_{iq} \end{bmatrix} \end{aligned} \]
注意,模型的决策变量向量为 \([\lambda_{1}, \cdots, \lambda_{n}, \theta]^T\);两个系数矩阵的主体部分都是原始指标数据的转置,约束条件可以对应地按分块矩阵合并来写: \[ \mathrm{s.t.}\quad \begin{bmatrix} X’\\ -Y’ \end{bmatrix}_{2\times1}\mathrm{\lambda}_{1\times1}\leqslant \begin{bmatrix}0\\-y’\end{bmatrix}_{2\times1} \]
(2) 产出导向的 CCR 模型
在给定产出条件下最小化投入,具体推导过程略,只列出最终的对偶模型:对每个决策单元 \(k\), \[ \begin{aligned}&\max\phi\\\mathbf{s.t.~~}&\sum_{i=1}^n\lambda_ix_{ij}\leq x_{kj}\\&\sum_{i=1}^n\lambda_iy_{ir}\geq\phi y_{kr}\\&\lambda_i\geq0,\quad j=1,\cdots,m;\;r=1,\cdots q\end{aligned} \]
该模型的效率为 \(1 / \phi\)。
11.2.2 BCC模型(规模收益可变假设下的径向 DEA 模型)
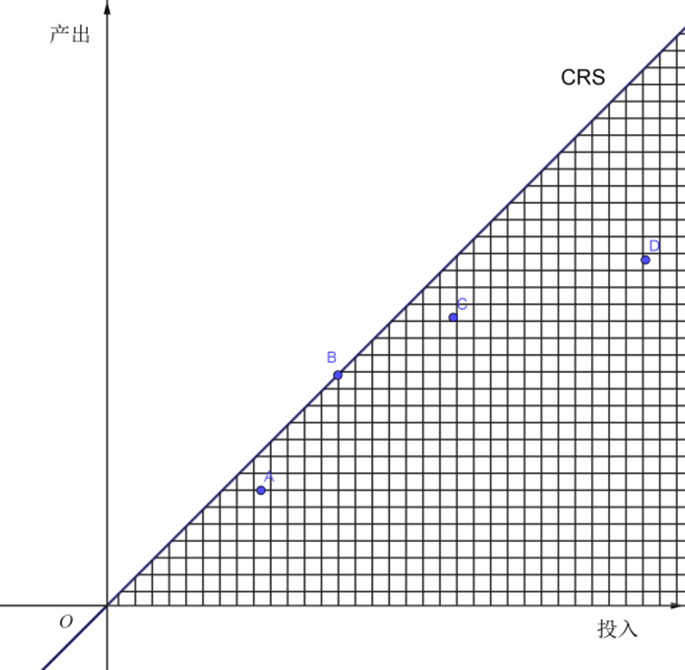
在 DEA 模型中,对规模收益(RTS)的设定决定了前沿的形状,CCR 模型是假设规模收益不变(CRS),即模型中的 \(\mathbf{\lambda}\) 满足 \(\mathbf{\lambda} > 0\),此时生产可能集(DEA 技术集)为以 OB 射线为前沿面的集合:
但在实际生产过程中,生产技术的规模收益并非 CRS,若采用 CRS 假设(CCR模型),得出的技术效率并非完全是纯技术效率,而是包含了规模效率成分的综合效率。
一般来说,生产技术的规模收益要先后经历规模收益递增(IRS)、规模收益不变(CRS)、规模收益递减(DRS)三个阶段。
如果无法确定研究样本处于哪个阶段,则评价技术效率时应选择规模收益可变(VRS)模型,即模型中的 \(\mathbf{\lambda}\) 满足 \(\sum \mathbf{\lambda} = 1\),此时生产可能集(DEA 技术集)为以线段 ABCD 以及 AD 往坐标轴的垂线为前沿(凸组合):
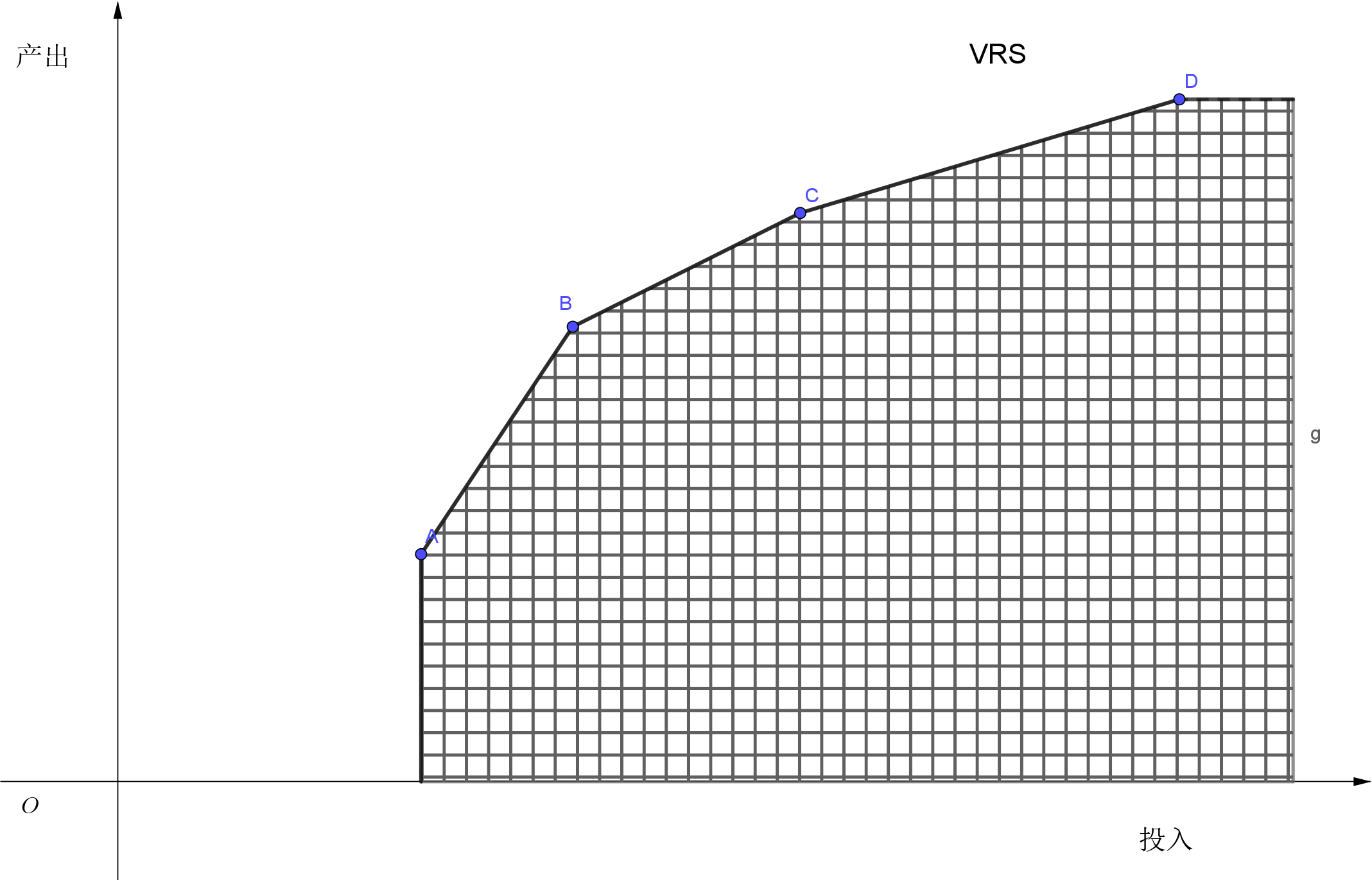
VRS 模型得出的技术效率是纯技术效率。
BCC 模型即规模收益可变(VRS)假设下的径向 DEA 模型,与 CCR 模型的区别就是增加了等式约束 \(\sum \mathbf{\lambda} = 1\)。
投入导向的 BCC(对偶)模型: 对每个决策单元 \(k\), \[ \begin{aligned}&\min\theta\\\mathbf{s.t.~~}&\sum_{i=1}^n\lambda_ix_{ij}\leq\theta x_{kj}\\&\sum_{i=1}^n\lambda_iy_{ir}\geq y_{kr}\\&\sum_{i=1}^n\lambda_i=1\\&\lambda_i\geq0,\quad j=1,\cdots,m;\;r=1,\cdots q\end{aligned} \]
产出导向的 BCC(对偶)模型: 对每个决策单元 \(k\), \[ \begin{aligned}&\max\phi\\\mathbf{s.t.}&\sum_{i=1}^n\lambda_ix_{ij}\leq x_{kj}\\&\sum_{i=1}^n\lambda_iy_{ir}\geq\phi y_{kr}\\&\sum_{i=1}^n\lambda_i=1\\&\lambda_i\geq0,\quad j=1,\cdots,m;\; r=1,\cdots q\end{aligned} \]
11.2.3 带非期望产出的 SBM 模型
在径向模型中,效率改善主要指的是投入或产出的等比例线性放缩,同时忽略了平行于坐标轴的弱有效的情形,而 SBM 模型纳入无效率的松弛改进,保证最终的结果是强有效的。
标准 SBM 模型形式为: 对每个决策单元 \(k\), \[ \begin{aligned}&\min\rho=\frac{1-\frac{1}{m}\sum_{j=1}^ms_j^-/x_{kj}}{1+\frac{1}{q}\sum_{r=1}^qs_r^-/y_{kj}}\\ \mathbf{s.t.~~}&X\lambda+s^-=x_k\\&Y\lambda-s^{+}=y_{k}\\&\lambda,s^-,s^+\geq0,\quad j=1,\cdots,m;\; r=1,\cdots,q\end{aligned} \]
该模型旨在通过最小化投入的相对减少量和最大化期望产出的相对增加量来衡量效率。目标函数最优解中 \(\rho^*\) 表示效率值,该模型同时从投入和产出两个方面考察无效率的表现,故称为非径向模型。
若同时加入非期望产出,则得到带非期望产出的 SBM 模型:对每个决策单元 \(k\), \[ \begin{aligned} & \min \rho = \frac{1 - \frac{1}{m} \sum_{i=1}^m \frac{s_i^-}{x_{ik}}}{1 + \frac{1}{q+b} \left( \sum\limits_{r=1}^q \frac{s_r^g}{y_{rk}^g} + \sum\limits_{t=1}^b \frac{s_t^b}{y_{tk}^b} \right)} \\ \mathbf{s.t.~~}& X\lambda + s^- = x_k \\ & Y^g\lambda - s^g = y_k^g \\ & Y^b\lambda + s^b = y_k^b \\ & \lambda, s^-, s^g, s^b \geq 0, \quad i=1,\ldots,m; r=1,\ldots,q; t=1,\ldots,b \end{aligned} \] 其中,\(m,q,b\) 分别为投入、期望产出、非期望产出的数量;
\(s^-,s^g,s^b\) 分别为投入、期望产出和非期望产出的松弛变量;
\(x_k,y_k^g,y_k^b\) 分别为第\(k\)个 DMU 的投入、期望产出和非期望产出;
\(X,Y^g,Y^b\) 分别为投入、期望产出和非期望产出的数据矩阵;
\(\lambda\) 为权重向量。
11.2.4 超效率模型
在传统的 DEA 模型中,效率前沿上的决策单元(DMU)都会被赋予效率值 \(1\),这意味着这些单位都被视为“最优”或“有效”的代表。然而,这种设定也带来了一个问题:无法进一步区分这些高效单元之间的相对表现。
超效率模型正是为了解这一问题而提出的。其核心思想是:将原本处于效率前沿的某个 DMU 从参考集中移除,再评估它在其余 DMU 所构成的新前沿面上的表现。这样做的结果是,原本效率为 \(1\) 的 DMU 现在可能会得到一个大于 \(1\) 的效率值,从而反映出它在“超越现有最佳实践”时的表现。
换句话说,超效率模型不是重新评估谁是有效的,而是衡量那些已经被认为是有效的 DMU 之间,谁更胜一筹。这使得我们可以在不改变原有 DEA 基本框架的前提下,对高效单元进行排序和深入比较,尤其适用于需要甄选标杆或识别领先实践者的场景。
超效率模型在实际应用中非常有用,例如在绩效评估、资源分配、政策制定等方面,帮助决策者识别真正具有引领作用的个体,并据此推广先进经验。
以投入导向的 BCC(对偶)模型改写为超效率模型为例:对每个决策单元 \(k\), \[ \begin{aligned} & \min \theta \\ \text{s.t.} \quad & \sum_{\substack{i=1\\i \neq k}}^n \lambda_i x_{ij} \leq \theta x_{kj}, \quad j = 1, \cdots, m \\ & \sum_{\substack{i=1\\i \neq k}}^n \lambda_i y_{ir} \geq y_{kr}, \quad r = 1, \cdots, q \\ & \sum_{\substack{i=1\\i \neq k}}^n \lambda_i = 1, \\ &\lambda_i \geq 0, \quad i \neq k \end{aligned} \]
mathmodels 包对 deaR 包中的相应函数做了封装,提供了四个函数:basic_DEA、super_DEA、basic_SBM 和 super_SBM,分别适用于不同类型的 DEA 或 SBM 模型变体:径向数据包络分析(DEA)模型(Charnes 等,1978;Banker 等,1984)和基于松弛变量测度的 SBM 模型(Tone,2001)计算效率得分提供了简化的操作接口,支持在规模报酬不变(CRS)或规模报酬可变(VRS)条件下,运行标准模型和超效率模型,并可选择性地处理非期望产出。
基本语法为(同其它函数):
-
data:数据框,第 1 列为 DMU 名字; -
inputs/outputs(包含ud_outputs):投入、产出的列名或列索引; -
ud_outputs:非期望产出位于产出中的位置索引,默认为NULL; -
orientation:设置导向:"io"(默认,投入导向)、"oo"(产出导向); -
rts:设置规模收益:"crs"(不变规模收益)、“vrs”`(默认,可变规模收益)。
11.2.5 Malmquist 指数
Malmquist 指数 是一种基于数据包络分析(DEA)框架、用于衡量决策单元(DMU)在不同时期之间全要素生产率变化的指标。它通过比较不同时间点的技术前沿,将生产率变化分解为 技术效率变化(Efficiency Change, EC) 和 技术进步(Technical Change, TC)。
该指数建立在 Shephard 距离函数 的基础上,适用于投入导向或产出导向模型。无论选择哪种导向,计算时均采用原始距离函数值,而非人为归一化的“效率得分”。
1. Shephard 距离函数的定义
- 投入导向距离函数 \(D_I^t(\mathbf{x},\mathbf{y})\) 表示:在保持产出 \(\mathbf{y}\) 不变的前提下,投入向量 \(\mathbf{x}\) 可以按比例缩小的最大倍数 \(\theta\),使得 \((\theta\mathbf{x}, \mathbf{y})\) 仍属于时期 \(t\) 的生产可能集 \(P^t\):
\[ D_I^t(\mathbf{x},\mathbf{y}) = \sup\left\{ \theta \geq 0 \mid (\theta\mathbf{x}, \mathbf{y}) \in P^t \right\} \]
此时,\(D_I^t \in (0,1]\),且当 \(D_I^t = 1\) 时表示技术有效;\(D_I^t < 1\) 表示存在投入冗余。该值即为 DEA 模型求解出的效率值 \(\theta^*\)。
- 产出导向距离函数 \(D_O^t(\mathbf{x},\mathbf{y})\) 表示:在保持投入 \(\mathbf{x}\) 不变的前提下,产出向量 \(\mathbf{y}\) 可以按比例放大的最大倍数 \(\eta\),使得 \((\mathbf{x}, \eta\mathbf{y})\) 仍属于时期 \(t\) 的生产可能集 \(P^t\): \[ D_O^t(\mathbf{x},\mathbf{y}) = \sup\left\{ \eta \geq 0 \mid (\mathbf{x}, \eta\mathbf{y}) \in P^t \right\} \]
此时,\(D_O^t \in [1,\infty)\),且当 \(D_O^t = 1\) 时表示技术有效;\(D_O^t > 1\) 表示存在产出不足。
📌 注意:尽管实践中常将产出导向的“效率评分”定义为 \(1/D_O^t \in (0,1]\) 以便解释,但在 Malmquist 指数的正式计算中,应直接使用原始的距离函数值 \(D_O^t \geq 1\),以保证理论一致性。
2. 生产可能集说明
这里的 生产可能集 \(P^t = \{(\mathbf{x},\mathbf{y}) \mid \mathbf{x} \text{ 可生产 } \mathbf{y}\}\) 是由 DEA 方法构建的技术集合,表示在时期 \(t\) 下所有可行的“投入-产出”组合。其边界构成生产前沿。
- 在 规模报酬不变(CRS) 假设下,技术集允许自由缩放;
- 在 规模报酬可变(VRS) 假设下,技术集限制了大规模扩张的有效性。
注:单投入单导出的生产可能集(DEA 技术集),就是如前文图示的前沿线(面)及其右下方的区域,可以是规模收益 CRS 或 VRS 假设下。
3. 跨期距离函数的构造
考虑两个相邻时期 \(t\) 和 \(t+1\),我们需要计算以下四个距离函数(统一使用同一导向,例如产出导向):
- \(D^t(\mathbf{x}^t, \mathbf{y}^t)\):用 \(t\) 期技术评估 \(t\) 期自身表现;
- \(D^{t+1}(\mathbf{x}^{t+1}, \mathbf{y}^{t+1})\):用 \(t+1\) 期技术评估 \(t+1\) 期自身表现;
- \(D^t(\mathbf{x}^{t+1}, \mathbf{y}^{t+1})\):将 \(t+1\) 期的数据投影到 \(t\) 期的技术前沿;
- \(D^{t+1}(\mathbf{x}^t, \mathbf{y}^t)\):将 \(t\) 期的数据投影到 \(t+1\) 期的技术前沿。
这些距离函数通过 DEA 模型分别求解,是构建 Malmquist 指数的基础。
4. 参照集的选择
Malmquist 指数需要比较不同时期的技术前沿(即生产可能集),因此必须明确:以哪些决策单元作为构建每个时期技术前沿的基础? 这就是所谓的“参照集”选择问题。
主要有三种构建方式:
- 同期参照集:每个时期的生产可能集仅基于该时期自身的观测数据构建,即各期技术前沿独立估计。距离函数的计算以当期样本为参考基准,不跨期混合数据。
- 序列参照集:技术前沿随时间逐步累积扩展,后期的技术集包含当前及之前所有时期的数据。由此构建的生产可能集具有非递减性,反映技术演进过程中对历史最佳实践的持续吸收。
- 全局参照集:将所有时间段的观测数据合并,共同构建一个跨期统一的“全局生产可能集”。该前沿代表整个样本期内的最优技术边界,不随时间变化,为所有时期提供一致的评估基准。
5. Malmquist 指数的定义
Malmquist 生产率指数(MI)定义为: \[ \text{MI}^t = \sqrt{ \frac{D^t(\mathbf{x}^{t+1}, \mathbf{y}^{t+1}) / D^t(\mathbf{x}^t, \mathbf{y}^t)} {D^{t+1}(\mathbf{x}^{t+1}, \mathbf{y}^{t+1}) / D^{t+1}(\mathbf{x}^t, \mathbf{y}^t)} } \] 其中:
- 若 \(\text{MI}^t > 1\):表示生产率提高;
- 若 \(\text{MI}^t = 1\):表示生产率不变;
- 若 \(\text{MI}^t < 1\):表示生产率下降。
6. CRS 与 VRS 假设下的分解差异
Malmquist 指数的分解结果会因是否假设 规模报酬不变(CRS) 或 规模报酬可变(VRS) 而有所不同。
(1) CRS 假设下的 Malmquist 分解
在 CRS 下,技术前沿满足线性齐次性,此时 Malmquist 指数仅反映:
- 技术效率变化(EC)
- 技术进步(TC)
没有进一步区分规模效应。
因此,CRS-Malmquist 指数分解为: \[ \text{MI}_{\text{CRS}}^t = \underbrace{\frac{D_{\text{CRS}}^{t+1}(\mathbf{x}^{t+1}, \mathbf{y}^{t+1})}{D_{\text{CRS}}^t(\mathbf{x}^t, \mathbf{y}^t)}}_{\text{EC}_{\text{CRS}}} \times \underbrace{\sqrt{ \frac{D_{\text{CRS}}^t(\mathbf{x}^{t+1}, \mathbf{y}^{t+1}) / D_{\text{CRS}}^{t+1}(\mathbf{x}^{t+1}, \mathbf{y}^{t+1})}{D_{\text{CRS}}^t(\mathbf{x}^t, \mathbf{y}^t) / D_{\text{CRS}}^{t+1}(\mathbf{x}^t, \mathbf{y}^t)} }}_{\text{TC}_{\text{CRS}}} \]
此版本捕捉的是“纯技术”层面的变化,但包含了规模效率变动的影响。
(2) VRS 假设下的 Malmquist 分解
在 VRS 下,技术前沿不再允许任意缩放,因此可以剔除规模效率变化的影响,得到 纯技术效率变化 和 纯技术进步。
VRS-Malmquist 指数为: \[ \text{MI}_{\text{VRS}}^t = \underbrace{\frac{D_{\text{VRS}}^{t+1}(\mathbf{x}^{t+1}, \mathbf{y}^{t+1})}{D_{\text{VRS}}^t(\mathbf{x}^t, \mathbf{y}^t)}}_{\text{PEC}} \times \underbrace{\sqrt{ \frac{D_{\text{VRS}}^t(\mathbf{x}^{t+1}, \mathbf{y}^{t+1}) / D_{\text{VRS}}^{t+1}(\mathbf{x}^{t+1}, \mathbf{y}^{t+1})}{D_{\text{VRS}}^t(\mathbf{x}^t, \mathbf{y}^t) / D_{\text{VRS}}^{t+1}(\mathbf{x}^t, \mathbf{y}^t)} }}_{\text{PTC}} \]
其中:
- \(\text{PEC}\):Pure Efficiency Change(纯技术效率变化)
- \(\text{PTC}\):Pure Technical Change(纯技术进步)
✅ 关键优势:VRS 分解排除了规模效率波动的干扰,更适合识别“管理改进”或“技术创新”的真实影响。
(3) 规模效率变化(SEC)的提取
通过 CRS 与 VRS 结果的对比,还可进一步计算 规模效率变化(SEC): \[
\text{SEC}^t = \frac{\text{EC}_{\text{CRS}}}{\text{PEC}} = \frac{D_{\text{CRS}}^{t+1}/D_{\text{CRS}}^t}{D_{\text{VRS}}^{t+1}/D_{\text{VRS}}^t}
\] 若 \(\text{SEC}^t > 1\):表示规模效率提升(更接近最优规模);
若 \(\text{SEC}^t < 1\):表示规模效率退化。
最终完整的 TFP 分解为:
\[ \text{MI}^t = \text{PEC} \times \text{PTC} \times \text{SEC} \]
这被称为 三重分解法,完整揭示了生产率增长的来源。
mathmodels 包提供了 malmquist() 计算跨时期的 Malmquist 指数及其分解,该函数是对 deaR 包中相关函数做了封装,更便于使用。基本语法:
-
data: 长格式数据框,第 1 列为决策单元,包含时期列 -
period, inputs, outputs: 时期、投入和产出对应的列索引或列名 -
orientation:"io"(投入导向),"oo"(产出导向,默认) -
rts:"vrs"(可变规模报酬,默认),"crs"(不变规模报酬) -
type1: 参照集:"cont"(当期),"seq"(序列)或"glob"(全局,默认) -
type2: 分解方法:"fgnz"(Färe 等,1994),"rd"(Ray 和 Desli,1997,默认),"gl"(广义 Malmquist)或"bias"(偏向性技术变化)
返回包含 Period、DMU、Malmquist 指数、EC(效率变化)、TC(技术变化)、PECH(纯效率变化)和 SECH(规模效率变化)的数据框。
11.3 DEA 案例
加载包:
案例数据:2011 年各省(市、自治区)医院的部分投入和产出指标。以床位数和卫生技术人员数作为投入,以诊疗人次数和入院人数作为产出,(可选)医疗废弃物作为非期望产出。
# A tibble: 31 × 6
DMU `床位数(万个)` `卫技人员数(万个)` `诊疗人次数(万人次)` `入院人数(万人)`
<chr> <dbl> <dbl> <dbl> <dbl>
1 安徽 14.1 13.3 6334. 439.
2 北京 8.76 12.9 10434. 188.
3 福建 8.99 9.39 7206. 309.
4 甘肃 6.67 5.31 2772. 171.
5 广东 24.6 28.9 29378. 799.
6 广西 95.8 10.6 6445. 326.
7 贵州 7.84 6.93 2911. 243.
8 海南 2.14 2.63 1269. 61.2
9 河北 18.8 18.4 8249. 568.
10 河南 24.0 23.1 11408. 704.
# ℹ 21 more rows
# ℹ 1 more variable: `医疗废弃物(万套)` <dbl>先以投入导向、VRS 假设下的 DEA 模型(BCC)为例,不考虑非期望产出:
- 查看各 DMU 效率值
安徽 北京 福建 甘肃 广东 广西 贵州 海南
0.9548803 0.9184863 1.0000000 0.8550507 1.0000000 0.7966680 0.9708290 0.9414552
河北 河南 黑龙江 湖北 湖南 吉林 江苏 江西
0.9390585 0.9615116 0.6900295 0.9703535 1.0000000 0.7418425 0.9602820 1.0000000
辽宁 内蒙古 宁夏 青海 山东 山西 陕西 上海
0.7314317 0.7214879 0.9100736 0.9074069 1.0000000 0.6190050 0.8281242 1.0000000
四川 天津 西藏 新疆 云南 浙江 重庆
1.0000000 1.0000000 1.0000000 1.0000000 1.0000000 0.9505551 0.8922566 -
bbc_in对象中还包含其它结果(略):
-
松弛变量(\(\mathbf{s}\)):衡量投入过度或产出不足的程度,反映决策单元在哪些方面可以进一步优化:
- 投入松弛 = 实际投入 - 目标投入
- 产出松弛 = 目标产出 - 实际产出
-
权重(\(\mathbf{\lambda}\)):表示参考单元的权重,用于构建效率前沿;每个 DMU 的效率值由其参考单元的线性组合计算:
- 对于非有效 DMU(效率值 \(< 1\)),\(\lambda\) 表示它应该向哪些有效 DMU(效率值 \(= 1\))学习,\(\lambda > 0\) 的 DMU 是其参考单元
-
目标值: DMU 达到 DEA 有效时应有的投入和产出水平;对非有效 DMU,目标值 = 参考单元的加权组合:
- 投入目标 = 实际投入 - 投入松弛
- 产出目标 = 实际产出 + 产出松弛
参照单元:效率前沿上的 DMU,非有效 DMU 通过模仿它们来提高效率;\(\lambda > 0\) 的 DMU。
-
规模收益:表示 DMU 的规模效率,基于 VRS 模型的 \(\lambda\) 值之和:
- irs(\(\sum \lambda < 1\)):规模报酬递增(扩大规模可提升效率)
- drs(\(\sum \lambda > 1\)):规模报酬递减(规模过大导致效率下降)
- crs(\(\sum \lambda = 1\)):规模报酬不变(最优规模)
若计算同样设置下的超效率:
安徽 北京 福建 甘肃 广东 广西 贵州 海南
0.9548803 0.9184863 1.0518247 0.8550507 NA 0.7966680 0.9708290 0.9414552
河北 河南 黑龙江 湖北 湖南 吉林 江苏 江西
0.9390585 0.9615116 0.6900295 0.9703535 1.0368439 0.7418425 0.9602820 1.0036738
辽宁 内蒙古 宁夏 青海 山东 山西 陕西 上海
0.7314317 0.7214879 0.9100736 0.9074069 NA 0.6190050 0.8281242 1.1885921
四川 天津 西藏 新疆 云南 浙江 重庆
1.0446519 1.0295240 2.9436174 1.0114148 1.1956914 0.9505551 0.8922566 注意,有些 DMU 的超效率为 NA,对应其线性规划模型无可行解,一种处理办法是将其替换为标准 DEA 效率值:
安徽 北京 福建 甘肃 广东 广西 贵州 海南
0.9548803 0.9184863 1.0518247 0.8550507 1.0000000 0.7966680 0.9708290 0.9414552
河北 河南 黑龙江 湖北 湖南 吉林 江苏 江西
0.9390585 0.9615116 0.6900295 0.9703535 1.0368439 0.7418425 0.9602820 1.0036738
辽宁 内蒙古 宁夏 青海 山东 山西 陕西 上海
0.7314317 0.7214879 0.9100736 0.9074069 1.0000000 0.6190050 0.8281242 1.1885921
四川 天津 西藏 新疆 云南 浙江 重庆
1.0446519 1.0295240 2.9436174 1.0114148 1.1956914 0.9505551 0.8922566 最后,再计算另外四种 DEA 效率:
ccr_in = basic_DEA(df, inputs = 2:3, outputs = 4:5,
orientation = "io", rts = "crs")
ccr_out = basic_DEA(df, inputs = 2:3, outputs = 4:5,
orientation = "oo", rts = "crs")
bbc_out = basic_DEA(df, inputs = 2:3, outputs = 4:5,
orientation = "oo", rts = "vrs")
sbm_ud_out = basic_SBM(df, inputs = 2:3, outputs = 4:6, ud_outputs = 3,
orientation = "oo", rts = "vrs")合并结果,并计算规模效率(CRS 效率 = VRS 效率 * 规模效率):
tibble(DMU = df$DMU, ccr_in = ccr_in$efficiencies,
ccr_out = ccr_out$efficiencies,
bbc_in = bbc_in$efficiencies,
bbc_out = bbc_out$efficiencies,
sbm_ud_out = sbm_ud_out$efficiencies,
scale_eff = ccr_in / bbc_in)# A tibble: 31 × 7
DMU ccr_in ccr_out bbc_in bbc_out sbm_ud_out scale_eff
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 安徽 0.944 0.944 0.955 0.957 0.690 0.989
2 北京 0.917 0.917 0.918 0.917 0.839 0.999
3 福建 1.00 1 1.00 1 1.000 1.000
4 甘肃 0.834 0.834 0.855 0.849 1 0.975
5 广东 1.000 1 1.00 1 1.000 1.000
6 广西 0.795 0.795 0.797 0.802 0.847 0.998
7 贵州 0.963 0.963 0.971 0.970 0.728 0.992
8 海南 0.833 0.833 0.941 0.932 0.771 0.885
9 河北 0.904 0.904 0.939 0.945 0.619 0.963
10 河南 0.883 0.883 0.962 0.970 0.841 0.918
# ℹ 21 more rows11.4 DEA-malmquist 案例
来自 deaR 包的 2005-2009 年中国各省份工业经济数据(长格式),共 155 行、5 列,包含决策单元(各省份)、年份,以及
投入指标:
-
Capital:总资产(亿元); -
Labor:年平均从业人员(万人)。
产出指标 :
-
GIOV:工业总产值(亿元)。
该数据集可评估中国工业部门在“十一五”期间的生产效率变化、技术进步与规模效益。数据结构清晰,适合进行跨期、跨区域的效率比较分析。
# A tibble: 155 × 5
DMUs Period Capital Labor GIOV
<chr> <dbl> <dbl> <dbl> <dbl>
1 Beijing 2005 12830. 117. 6946.
2 Tianjin 2005 6348. 122. 6774.
3 Hebei 2005 9474. 292. 11008.
4 Shanxi_1 2005 7045. 213. 4851.
5 Neimenggu 2005 4596. 83.7 2996.
6 Liaoning 2005 11902. 277. 10815.
7 Jilin 2005 4507. 102. 3792.
8 Heilongjiang 2005 5174. 137. 4715.
9 Shangai 2005 15906. 260. 15768.
10 Jiangsu 2005 25489. 704. 32707.
# ℹ 145 more rows调用 malmquist() 函数计算 Malmquist 指数及其分解,需要提供长格式数据框,设置日期、投入、产出列,可选提供导向、规模收益假设、参照集、计算方法:
malmquist(dat, period = 2, inputs = 3:4, outputs = 5,
orientation = "oo", rts = "vrs",
type1 = "glob", type2 = "rd")# A tibble: 124 × 7
Period DMU mi ec tc pech sech
<chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 2005~2006 Beijing 1.18 0.970 1.22 0.970 1.00
2 2005~2006 Tianjin 1.22 0.993 1.23 1.00 0.993
3 2005~2006 Hebei 1.03 0.979 1.05 0.977 1.00
4 2005~2006 Shanxi_1 0.969 0.939 1.03 0.935 1.00
5 2005~2006 Neimenggu 1.20 0.987 1.22 0.990 0.997
6 2005~2006 Liaoning 1.13 1.01 1.11 1.01 1.000
7 2005~2006 Jilin 1.10 0.956 1.15 0.950 1.01
8 2005~2006 Heilongjiang 1.05 0.966 1.09 0.963 1.00
9 2005~2006 Shangai 1.12 0.990 1.13 1.00 0.990
10 2005~2006 Jiangsu 0.942 0.891 1.06 1 0.891
# ℹ 114 more rowsmi 为 Malmquist 指数,ec 为技术效率变化,tc 为技术进步,pech 为纯技术效率变化,sech 为规模效率变化。
更多的 DEA 模型还有:考虑环境因素和随机噪声对决策单元效率影响的三阶段 DEA 模型;固定前沿生产函数的参数法随机前沿模型;以及以效率为因变量研究效率的影响因素的 Tobit 回归模型。